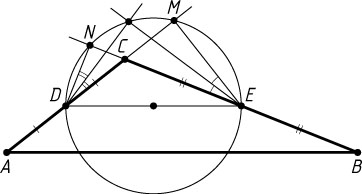
3483. Точки D
и E
— середины сторон соответственно AC
и BC
треугольника ABC
. На отрезке DE
как на диаметре построена окружность, пересекающая продолжения сторон AC
и BC
в точках M
и N
соответственно.
а) Докажите, что биссектрисы углов MEN
и NDM
пересекаются на этой окружности.
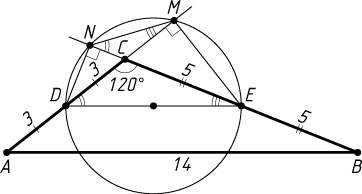
б) Найдите MN
, если известно, что AB=14
, BC=10
, AC=6
.
Ответ. 3,5.
Решение. а) Биссектриса вписанного угла проходит через середину дуги, на которую этот угол опирается. Значит, биссектрисы вписанных углов MEN
и NDM
(рис. 1) проходят через середину дуги MN
, не содержащей точки D
.
б) По теореме косинусов находим (рис. 2), что
\cos\angle ACB=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC\cdot BC}=\frac{36+100-196}{2\cdot6\cdot10}=-\frac{1}{2}.
Значит, \angle ACB=120^{\circ}
.
Отрезок DE
— средняя линия треугольника ABC
, поэтому DE=\frac{1}{2}AB
. Треугольники CMN
и CED
подобны по двум углам, причём коэффициент подобия равен \frac{CM}{CE}=\cos60^{\circ}=\frac{1}{2}
(см. задачу 19). Следовательно, MN=\frac{1}{2}DE=\frac{1}{4}AB=3{,}5
.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 15.23.1, с. 161
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. —

