3484. Окружность, вписанная в треугольник ABC
, касается его сторон BC
, AC
и AB
в точках A_{1}
, B_{1}
и C_{1}
соответственно. В треугольнике A_{1}B_{1}C_{1}
проведены высоты.
а) Докажите, что треугольник с вершинами в основаниях этих высот подобен треугольнику ABC
.
б) Найдите коэффициент подобия, если известно, что радиус вписанной окружности треугольника ABC
в три раза меньше радиуса описанной.
Ответ. \frac{1}{6}
.
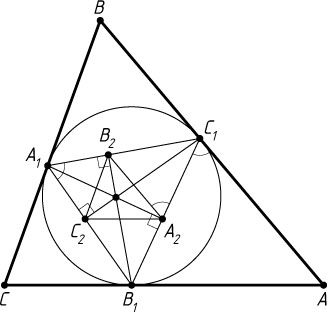
Решение. а) A_{1}A_{2}
и B_{1}B_{2}
— высоты треугольника A_{1}B_{1}C_{1}
(рис. 1), поэтому \angle C_{1}A_{2}B_{2}=\angle C_{1}A_{1}B_{1}
, а из теоремы об угле между касательной и хордой следует, что \angle C_{1}A_{1}B_{1}=\angle AC_{1}B_{1}
. Значит, A_{2}B_{2}\parallel AB
. Аналогично, A_{2}C_{2}\parallel AC
и B_{2}C_{2}\parallel BC
.
Стороны треугольника A_{2}B_{2}C_{2}
соответственно параллельны сторонам треугольника ABC
, значит, углы этих треугольников соответственно равны. Следовательно, треугольники подобны.
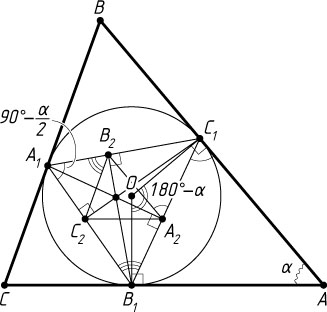
б) Пусть r
и R
— радиусы соответственно вписанной и описанной окружностей треугольника ABC
, O
— центр вписанной окружности (рис. 2). Обозначим \angle BAC=\alpha
. Тогда
\angle B_{1}OC_{1}=180^{\circ}-\alpha,~\angle B_{1}A_{1}C_{1}=\frac{1}{2}\angle B_{1}OC_{1}=90^{\circ}-\frac{\alpha}{2}.
По теореме синусов
B_{1}C_{1}=2r\sin\left(90^{\circ}-\frac{\alpha}{2}\right)=2r\cos\frac{\alpha}{2},~BC=2R\sin\alpha,
а так как треугольник A_{1}B_{2}C_{2}
подобен треугольнику A_{1}B_{1}C_{1}
(см. задачу 19) с коэффициентом \cos\angle B_{1}A_{1}C_{1}=\cos\left(90^{\circ}-\frac{\alpha}{2}\right)=\sin\frac{\alpha}{2}
, то B_{2}C_{2}=B_{1}C_{1}\sin\frac{\alpha}{2}
.
Пусть k
— коэффициент подобия треугольников A_{2}B_{2}C_{2}
и ABC
. Тогда
k=\frac{B_{2}C_{2}}{BC}=\frac{B_{1}C_{1}\sin\frac{\alpha}{2}}{2R\sin\alpha}=\frac{2r\cos\frac{\alpha}{2}\sin\frac{\alpha}{2}}{2R\sin\alpha}=\frac{r\sin\alpha}{2R\sin\alpha}=\frac{1}{2}\cdot\frac{r}{R}=\frac{1}{2}\cdot\frac{1}{3}=\frac{1}{6}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. —

