3575. Дан угол XAY
и точка O
внутри него. Проведите через точку O
прямую, отсекающую от данного угла треугольник наименьшей площади.
Указание. Через точку O
проведите прямую, отрезок которой, заключённый внутри данного угла, делился бы точкой O
пополам.
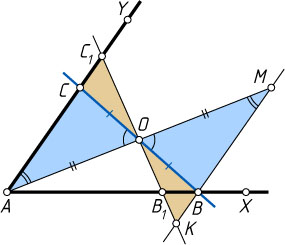
Решение. На продолжении отрезка AO
за точку O
отложим отрезок OM
, равный OA
, и проведём через точку M
прямую, параллельную стороне AY
данного угла. Пусть B
— точка пересечения этой прямой со стороной AX
, а прямая BO
пересекает сторону AY
в точке C
. Тогда треугольники MOB
и AOC
равны по стороне и двум прилежащим к ней углам. Поэтому OB=OC
. Докажем, что ABC
— искомый треугольник.
Первый способ. Проведём через точку O
прямую, пересекающую AX
и AY
в точках B_{1}
и C_{1}
соответственно. Пусть B_{1}
лежит между A
и B
. Обозначим через K
точку пересечения прямых B_{1}C_{1}
и MB
. Тогда
S_{\triangle OB_{1}B}=S_{\triangle OKB}-S_{\triangle B_{1}KB}\lt S_{\triangle OKB}=S_{\triangle OCC_{1}}.
Следовательно, S_{\triangle ABC}\lt S_{\triangle AB_{1}C_{1}}
.
Случай, когда точка B
лежит между точками A
и B_{1}
рассматривается аналогично.
Второй способ. Проведём через точку O
прямую. Пусть X
и Y
— точки её пересечения со сторонами данного угла, а точки P
и Q
лежат на сторонах AX
и AY
, причём APOQ
— параллелограмм. Обозначим S_{\triangle OXP}=S_{1}
и S_{\triangle OYQ}=S_{2}
. Тогда
S_{APOQ}=2\sqrt{S_{1}S_{2}}
(см. задачу 3029), поэтому
S_{\triangle XAY}=S_{1}+S_{2}+S_{APOQ}=S_{1}+S_{2}+2\sqrt{S_{1}S_{2}}\geqslant
\geqslant2\sqrt{S_{1}S_{2}}+2\sqrt{S_{1}S_{2}}=4\sqrt{S_{1}S_{2}},
причём равенство достигается, когда S_{1}=S_{2}
, т. е. если O
— середина XY
. Следовательно, в этом случае точки X
и Y
совпадают с построенными ранее точками A
и B
соответственно.
Источник: Московская математическая олимпиада. — 1946, IX, 1-й тур, 9-10 классы
Источник: Зетель С. И. Задачи на максимум и минимум. — М.—Л.: ОГИЗ, Гостехиздат, 1948. — № 8, с. 15
Источник: Вступительный экзамен в МФТИ. — 1954, билет 15, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 54-15-1, с. 48
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 7, с. 29
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 142, с. 52
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 11.24, с. 285
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 11.24, с. 275
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 161
