3601. Две стороны треугольника равны 10 и 15. Докажите, что биссектриса угла между ними не больше 12.
Указание. Через основание биссектрисы проведите прямую, параллельную одной из данных сторон треугольника; воспользуйтесь свойством биссектрисы треугольника.
Решение. Первый способ. Обозначим стороны BC
и AC
треугольника ABC
через a
и b
соответственно, а его биссектрису CD
— через x
(в данном случае a=10
, b=15
).
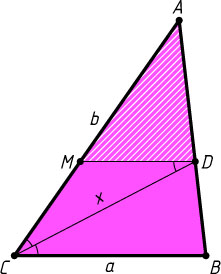
Через точку D
проведём прямую, параллельную стороне BC
, до пересечения со стороной AC
в точке M
(рис. 1). Тогда
\angle MDC=\angle BCD=\angle DCM.
Поэтому треугольник DCM
— равнобедренный. Из подобия треугольников ADM
и ABC
находим, что
DM=BC\cdot\frac{AD}{AB}=\frac{ab}{a+b}
(так как \frac{AD}{BD}=\frac{AC}{BC}=\frac{b}{a}
). Следовательно,
x=CD\lt CM+DM=2DM=\frac{2ab}{a+b}=2\cdot10\cdot\frac{15}{10+15}=12.
Второй способ. Обозначим стороны BC
и AC
треугольника ABC
через a
и b
соответственно, а его биссектрису CD
— через x
(в данном случае a=10
, b=15
). По свойству биссектрисы треугольника
\frac{BD}{DA}=\frac{BC}{AC}=\frac{a}{b}.
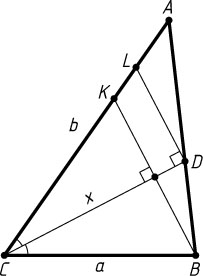
Через точки B
и D
проведём прямые, перпендикулярные биссектрисе CD
, до пересечения с прямой AC
в точках K
и L
соответственно (рис. 2). Тогда треугольник BCK
— равнобедренный (его высота и биссектриса, проведённые из вершины C
, совпадают). Поэтому
AK=AC-CK=AC-BC=b-a,~\frac{KL}{LA}=\frac{BD}{DA}=\frac{a}{b}.
Следовательно,
KL=AK\cdot\frac{a}{a+b}=\frac{a(b-a)}{a+b},
CL=CK+KL=CB+KL=a+\frac{a(b-a)}{a+b}=\frac{2ab}{a+b}=2\cdot10\cdot\frac{15}{10+15}=12,
x=CD\lt CL=12.
Третий способ. Обозначим стороны BC
и AC
треугольника ABC
через a
и b
соответственно, а его биссектрису CD
— через x
(в данном случае a=10
, b=15
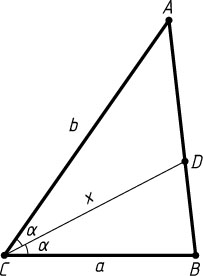
), \angle ACB=2\alpha
(рис. 3). Тогда
x=\frac{2ab\cos\alpha}{a+b}
(см. задачу 4021). Следовательно,
CB=x\lt\frac{2ab}{a+b}=2\cdot10\cdot\frac{15}{10+15}=12.
Примечание. Верно следующее общее общее утверждение. Если стороны треугольника равны a
и b
, а биссектриса треугольника, проведённая к третьей стороне, равна l
, то l\lt\frac{2ab}{a+b}
, т. е. эта биссектриса меньше среднего гармонического сторон a
и b
.
Автор: Васильев Н. Б.
Источник: Журнал «Квант». — 1971, № 4, с. 33, М77
Источник: Задачник «Кванта». — М77


