3656. Докажите, что площадь треугольника с вершинами в серединах высот треугольника ABC
в четыре раза меньше площади ортотреугольника треугольника ABC
.
Указание. Середины высот треугольника ABC
лежат на его средних линиях. Далее см. задачу 3800.
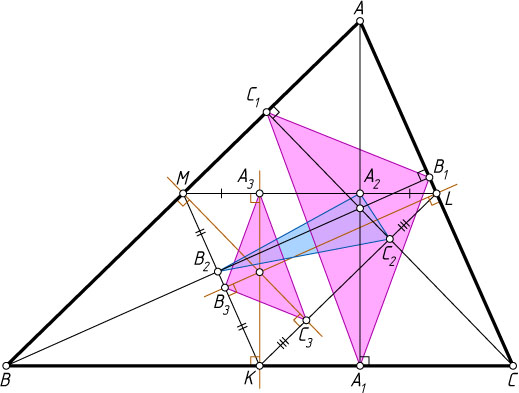
Решение. Пусть A_{2}
, B_{2}
и C_{2}
— середины высот соответственно AA_{1}
, BB_{1}
и CC_{1}
треугольника ABC
, точки K
, L
и M
— середины сторон BC
, AC
и AB
соответственно.
Пусть серединный перпендикуляр к стороне BC
пересекается с прямой ML
в точке A_{3}
. Средняя линия ML
треугольника ABC
проходит через середину A_{2}
высоты AA_{1}
, а так как прямоугольные треугольники AA_{2}M
и KA_{3}L
равны по гипотенузе и острому углу, то A_{2}M=A_{3}L
. Значит, точки A_{2}
и A_{3}
симметричны относительно середины стороны ML
треугольника KLM
. Аналогично определим точки B_{3}
и C_{3}
и докажем, что они симметричны точкам B_{2}
и C_{2}
относительно середин сторон соответственно MK
и KL
треугольника KLM
.
Треугольник KLM
подобен треугольнику ABC
с коэффициентом \frac{1}{2}
, значит, ортотреугольник A_{3}B_{3}C_{3}
треугольника KLM
подобен ортотреугольнику A_{1}B_{1}C_{1}
треугольника ABC
с тем же коэффициентом. Треугольник A_{2}B_{2}C_{2}
равновелик треугольнику A_{3}B_{3}C_{3}
(см. задачу 3800), а площадь треугольника A_{3}B_{3}C_{3}
в четыре раза меньше площади треугольника A_{1}B_{1}C_{1}
. Следовательно, и площадь треугольника A_{2}B_{2}C_{2}
в четыре раза меньше площади треугольника A_{1}B_{1}C_{1}
. Что и требовалось доказать.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — № 19, с. 24
