3800. Точки A_{1}
, B_{1}
и C_{1}
лежат на сторонах соответственно BC
, AC
и AB
треугольника ABC
, точки A_{2}
, B_{2}
и C_{2}
соответственно симметричны точкам A_{1}
, B_{1}
и C_{1}
относительно середин сторон, на которых они лежат. Докажите, что треугольники A_{1}B_{1}C_{1}
и A_{2}B_{2}C_{2}
равновелики.
Решение. Поскольку
S_{\triangle A_{1}B_{1}C_{1}}=S_{\triangle ABC}-S_{\triangle AB_{1}C_{1}}-S_{\triangle BA_{1}C_{1}}-S_{\triangle CA_{1}B_{1}},
S_{\triangle A_{2}B_{2}C_{2}}=S_{\triangle ABC}-S_{\triangle AB_{2}C_{2}}-S_{\triangle BA_{2}C_{2}}-S_{\triangle CA_{2}B_{2}},
достаточно доказать, что
S_{\triangle AB_{1}C_{1}}+S_{\triangle BA_{1}C_{1}}+S_{\triangle CA_{1}B_{1}}=S_{\triangle AB_{2}C_{2}}+S_{\triangle BA_{2}C_{2}}+S_{\triangle CA_{2}B_{2}}
Пусть площадь треугольника ABC
равна 1. Обозначим
BC=a,~AC=b,~AB=c,~AC_{1}=BC_{2}=x,~AB_{2}=CB_{1}=y,~BA_{1}=CA_{2}=z.
Тогда
S_{\triangle AB_{1}C_{1}}=\frac{AC_{1}}{AB}\cdot\frac{AB_{2}}{AC}=\frac{x}{c}\cdot\frac{b-y}{b}=\frac{x}{c}\left(1-\frac{y}{b}\right)=\frac{x}{c}-\frac{x}{c}\cdot\frac{y}{b}.
Аналогично
S_{\triangle BA_{1}C_{1}}=\frac{z}{a}-\frac{z}{a}\cdot\frac{x}{c},~S_{\triangle CA_{1}B_{1}}=\frac{y}{b}-\frac{y}{b}\cdot\frac{z}{a},
S_{\triangle AB_{2}C_{2}}=\frac{y}{b}-\frac{y}{b}\cdot\frac{x}{c},~S_{\triangle BA_{2}C_{2}}=\frac{x}{c}-\frac{x}{c}\cdot\frac{z}{a},~S_{\triangle CA_{2}B_{2}}=\frac{z}{a}-\frac{z}{a}\cdot\frac{y}{b}.
Следовательно,
S_{\triangle AB_{1}C_{1}}+S_{\triangle BA_{1}C_{1}}+S_{\triangle CA_{1}B_{1}}=\frac{x}{c}-\frac{x}{c}\cdot\frac{y}{b}+\frac{z}{a}-\frac{z}{a}\cdot\frac{x}{c}+\frac{y}{b}-\frac{y}{b}\cdot\frac{z}{a}=
=\frac{y}{b}-\frac{y}{b}\cdot\frac{x}{c}+\frac{x}{c}-\frac{x}{c}\cdot\frac{z}{a}+\frac{z}{a}-\frac{z}{a}\cdot\frac{y}{b}=S_{\triangle AB_{2}C_{2}}+S_{\triangle BA_{2}C_{2}}+S_{\triangle CA_{2}B_{2}}.
Что и требовалось доказать.
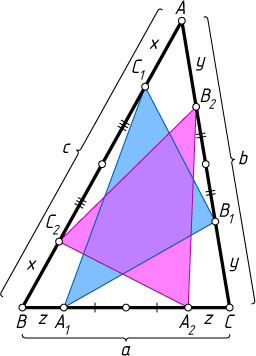
Примечание. Используя понятие изотомическая точка (см. замечание к задаче 2415), эту задачу можно сформулировать так. На сторонах треугольника взяты изотомические точки A_{1}
и A_{2}
, B_{1}
и B_{2}
, C_{1}
и C_{2}
. Докажите, что треугольники A_{1}B_{1}C_{1}
и A_{2}B_{2}C_{2}
равновелики.
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 99
