3802. Докажите, что сумма квадрата расстояния от точки пересечения высот (ортоцентра) треугольника до вершины и квадрата противоположной стороны равна квадрату диаметра описанной окружности треугольника.
Указание. Расстояние от ортоцентра треугольника до его вершины вдвое больше расстояния от центра описанной окружности до противоположной стороны (см. задачу 1257).
Решение. Заметим, что для прямоугольного треугольника утверждение очевидно. Рассмотрим случай не прямоугольного треугольника.
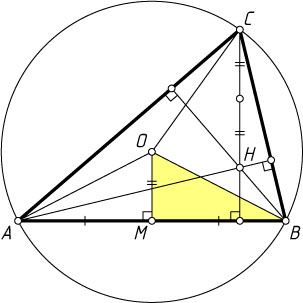
Пусть H
— точка пересечения высот треугольника ABC
, O
— центр описанной окружности радиуса R
, M
— середина стороны BC
. Известно (см. задачу 1257), что расстояние от ортоцентра треугольника до его вершины вдвое больше расстояния от центра описанной окружности до противоположной стороны, поэтому OM=\frac{1}{2}AH
. Применив теорему Пифагора к прямоугольному треугольнику OMB
, получим, что OM^{2}+BM^{2}=OB^{2}
, или \frac{AH^{2}}{4}+\frac{BC^{2}}{4}=OB^{2}
. Следовательно, AH^{2}+BC^{2}=4OB^{2}=4R^{2}
. Что и требовалось доказать.
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 233, с. 23
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 87
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 4.11, с. 42
