3952. Пусть ABC
— правильный треугольник. На его стороне AC
выбрана точка T
, а на дугах AB
и BC
его описанной окружности выбраны точки M
и N
соответственно так, что MT\parallel BC
и NT\parallel AB
. Отрезки AN
и MT
пересекаются в точке X
, а отрезки CM
и NT
— в точке Y
. Докажите, что периметры многоугольников AXYC
и XMBNY
равны.
Указание. Если точка P
лежит на меньшей дуге BC
окружности, описанной около равностороннего треугольника ABC
, то что AP=BP+CP
(теорема Помпею).
Решение. Воспользуемся следующим известным фактом: если точка P
лежит на меньшей дуге BC
окружности, описанной около равностороннего треугольника ABC
, то что AP=BP+CP
(см. 17, теорема Помпею).
По условию задачи MT\parallel BC
и NT\parallel AB
, поэтому
\angle ATM=\angle ACB=60^{\circ},~\angle CTN=\angle CAB=60^{\circ},\angle MTY=\angle MTN=60^{\circ},
а так как вписанные углы AMC
и ABC
опираются на одну и ту же дугу, то
\angle AMY=\angle AMC=\angle ABC=60^{\circ}.
Значит,
\angle AMY+\angle ATY=60^{\circ}+120^{\circ}=180^{\circ}.
Следовательно, около четырёхугольника AMYT
можно описать окружность. В эту окружность вписан правильный треугольник AMY
(\angle MAY=\angle MTY=60^{\circ}=AMY
), а точка T
лежит на меньшей дуге AY
, значит, AT+TY=MT=MX+TX
(см. задачу 17). Аналогично докажем, что CT+TX=NT=NY+TY
. Сложив эти два равенства, получим, что MX+NY=AT+CT=AC
.
Точка M
лежит на меньшей дуге AB
окружности, описанной около правильного треугольника ABC
, поэтому MA+MB=MC=MY+YC
, а так как MA=MY
, то MB=YC
. Аналогично получим, что BN=AX
.
Следовательно,
P_{AXYC}=AC+AX+CY+XY=(MX+NY)+BN+MB+XY=P_{XMBNY}.
Что и требовалось доказать.
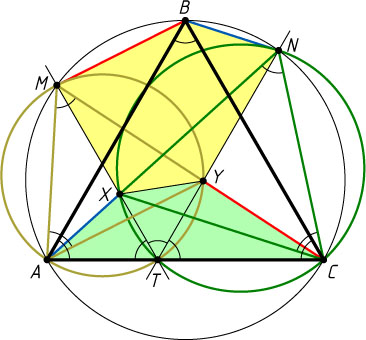
Автор: Шмаров В. А.
Источник: Всероссийская олимпиада школьников. — 2010-11, XXXVII, заключительный этап, 9 класс
Источник: Журнал «Квант». — 2011, № 5-6, с. 47
