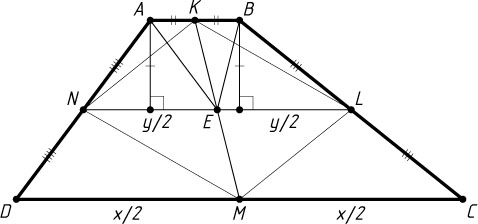
3992. В выпуклом четырёхугольнике ABCD
точки K
, L
, M
, N
— середины сторон AB
, BC
, CD
, DA
соответственно. Отрезки KM
и LN
пересекаются в точке E
. Площади четырёхугольников AKEN
, BKEL
и DNEM
равны соответственно 6, 6 и 12. Найдите:
а) площадь четырёхугольника CMEL
;
б) отрезок CD
, если AB=\frac{1}{2}
.
Ответ. а) 12; б) \frac{5}{2}
.
Указание. Докажите, что данный четырёхугольник — трапеция.
Решение. Известно, что середины сторон любого четырёхугольника являются вершинами параллелограмма (см. задачу 1204). Поэтому KLMN
— параллелограмм (рис. 1). Значит, E
— середина LN
. Поскольку EK
— медиана треугольника AEB
, то треугольники AEK
и BEK
равновелики, а так как равновелики четырёхугольники AKEN
и BKEL
, то S_{\triangle AEN}=S_{\triangle BEL}
. Основания NE
и LE
равновеликих треугольников AEN
и BEL
равны, значит равны их высоты, опущенные на эти основания. Таким образом, точки A
и B
равноудалены от прямой NL
. Следовательно, LN\parallel AB
.
Поскольку L
и N
— середины отрезков BC
и AD
, то CD\parallel AB
. Значит, ABCD
и CDNL
— трапеции. Поскольку точки E
и M
— середины оснований трапеции CDNL
, то S_{CMEL}=S_{DNEM}=12
.
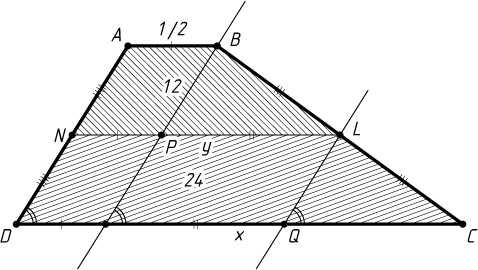
Пусть прямая, проходящая через вершину B
параллельно AD
, пересекает NL
в точке P
(рис. 2), а прямая, проходящая через точку L
параллельно AD
, пересекает CD
в точке Q
. Из равенства треугольников BPL
и LQC
следует, что LP=CQ
.
Обозначим CD=x
, LN=y
. Тогда
LP=NL-NP=NL-AB=y-\frac{1}{2},
CQ=CD-DR=CD-LN=x-y.
Поэтому x-y=y-\frac{1}{2}
. Поскольку площадь трапеции CDNL
вдвое больше площади трапеции ABLN
, то
\frac{1}{2}(x+y)=2\cdot\frac{1}{2}\left(y+\frac{1}{2}\right).
Из системы
\syst{2y-x=\frac{1}{2}\\x-y=1\\}
находим, что x=\frac{5}{2}
.
Источник: Вступительный экзамен на географический факультет МГУ. — 2004 (июль), вариант 1, № 4
Источник: Вступительные экзамены и олимпиады по математике 2003—2005 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2006. — с. 147

