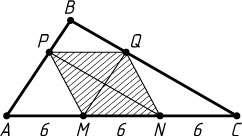
4017. В треугольник со сторонами 9 и 15 вписан параллелограмм так, что одна из его сторон, равная 6, лежит на третьей стороне треугольника, а диагонали параллелограмма параллельны двум данным сторонам треугольника. Найдите другую сторону параллелограмма и третью сторону треугольника.
Ответ. 4\sqrt{2}
, 18.
Указание. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Решение. Пусть вершины M
и N
параллелограмма MNQP
находятся на стороне AC
треугольника ABC
, а вершины P
и Q
— на сторонах AB
и AC
(AB=9
, BC=15
).
Поскольку APQM
и NPQC
— параллелограммы, то
AM=PQ=NC=6,~AC=18.
Из подобия треугольников CMQ
и CAB
следует, что
QM=\frac{2}{3}AB=6,
а из подобия треугольников APN
и ABC
—
PN=\frac{2}{3}BC=10.
Рассмотрим параллелограмм MNQP
. По теореме о сумме квадратов диагоналей параллелограмма (см. задачу 4011)
PN^{2}+MQ^{2}=2PQ^{2}+2PM^{2}.
Следовательно,
PM^{2}=\frac{1}{2}(PN^{2}+MQ^{2}-2PQ^{2})=\frac{1}{2}(100+36-72)=32.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.232, с. 174
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.8, с. 23
