4123. Докажите, что в прямоугольном треугольнике центр вписанной окружности, середина катета и точка касания другого катета с вневписанной окружностью лежат на одной прямой.
Решение. Первый способ. Пусть вписанная в треугольник ABC
окружность радиуса r
с центром I
касается катетов AC=b
и BC=a
в точках P
и M
соответственно, K
— середина AC
, N
— точка касания вневписанной окружности треугольника с катетом BC
. Достаточно доказать, что S_{CKIN}=S_{\triangle CKN}
.
Поскольку BN=CM
(см. задачу 4805),
CN=BC-BN=a-r,~S_{\triangle CIN}=\frac{1}{2}CN\cdot IM=\frac{1}{2}(a-r)r.
Тогда
S_{CKIN}=S_{\triangle CIN}+S_{\triangle CIK}=\frac{1}{2}(a-r)r+\frac{1}{2}\left(\frac{1}{2}b-r\right)r=
=\frac{1}{4}(2ar+br-2r^{2}),
S_{\triangle CKN}=\frac{1}{2}CN\cdot CK=\frac{1}{2}(a-r)\cdot\frac{b}{2}=\frac{1}{4}(ab-br).
Докажем, что
\frac{1}{4}(2ar+br-2r^{2})=\frac{1}{4}(ab-br).
Действительно, пусть полупериметр треугольника ABC
равен p
. Тогда
2ar+br-2r^{2}=ab-br~\Leftrightarrow~ar+br-r^{2}=\frac{ab}{2}~\Leftrightarrow
\Leftrightarrow~(a+b-r)r=\frac{ab}{2}~\Leftrightarrow~pr=S_{\triangle ABC}.
Следовательно, S_{CKIN}=S_{\triangle CKN}
. Что и требовалось доказать.
Второй способ. Пусть вписанная в треугольник ABC
окружность с центром I
касается катета BC
в точке M
, а вневписанная окружность — в точке N
.
Рассмотрим гомотетию с центром A
, при которой вневписанная окружность треугольника ABC
, касающаяся стороны BC
, переходит в его вписанную окружность. Точка N
при этом переходит в точку L
касания вписанной окружности и прямой, параллельной BC
, т. е. в точку, диаметрально противоположную точке M
. Поскольку AC\parallel LM
, продолжение медианы NI
треугольника MNL
пересекает катет AC
в его середине K
. Отсюда следует решение задачи.
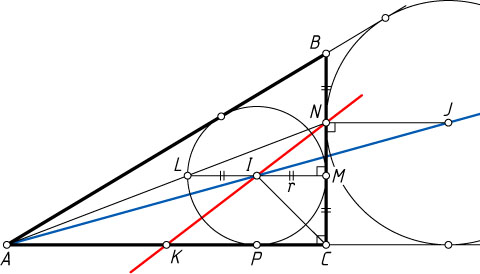
Примечание. См. статью А.Карлюченко и Г.Филипповского «Об одной замечательной прямой в треугольнике», Квант, 2007, N4, с.31, 34-35.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 5.4, с. 47
Источник: Журнал «Квант». — 2007, № 4, с. 35, задача 12
