4197. Пусть a
— длина стороны правильного пятиугольника, d
— длина его диагонали. Докажите, что d^{2}=a^{2}+ad
.
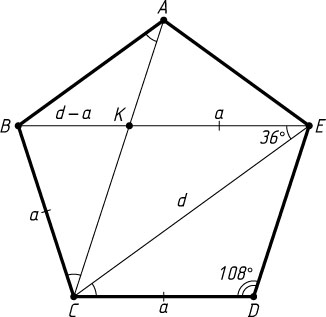
Указание. Пусть ABCDE
— правильный пятиугольник, K
— точка пересечения диагоналей BE
и AC
. Докажите, что треугольники BCK
и BEC
подобны (или примените теорему Птолемея к вписанному четырёхугольнику ABCD
).
Решение. Первый способ. Пусть K
— точка пересечения диагоналей BE
и AC
правильного пятиугольника ABCDE
.
Каждый угол правильного пятиугольника равен \frac{180^{\circ}(5-2)}{5}=\frac{540^{\circ}}{5}=108^{\circ}
, а угол между диагоналями, исходящими из одной вершины, равен \frac{360^{\circ}}{2\cdot5}=36^{\circ}
. Значит,
\angle KCB=\angle ACB=\angle BAC=\frac{180^{\circ}-\angle ABC}{2}=\frac{180^{\circ}-108^{\circ}}{2}=36^{\circ}=\angle BEC,
поэтому треугольники BCK
и BEC
подобны по двум углам (угол CBE
— общий).
Кроме того,
\angle DCE=\angle ACB=36^{\circ}=\angle BEC,
значит, BE\parallel CD
. Аналогично, DE\parallel AC
, следовательно, четырёхугольник CDEK
— параллелограмм, поэтому EK=CD=a
.
Из подобия треугольников BCK
и BEC
получим, что \frac{BK}{BC}=\frac{BC}{BE}
, откуда BC^{2}=BK\cdot BE
, или
a^{2}=(BE-EK)BE=(d-a)d=d^{2}-ad.
Следовательно, d^{2}=a^{2}+ad
, или \frac{d}{a}-\frac{a}{d}=1
.
Второй способ. Пусть ABCDE
— правильный пятиугольник со стороной a
и диагональю d
. Применив к вписанному четырёхугольнику ABCD
теорему Птолемея (см. задачу 130), получим
AC\cdot BD=AB\cdot CD+BC\cdot AD,~\mbox{или}~d^{2}=a^{2}+ad.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 6.45(б)
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.49(б), с. 156
Источник: Журнал «Crux Mathematicorum». — 2018, задача CC292, с. 368
