4302. Дан равносторонний треугольник ABC
. Из его внутренней точки M
опущены перпендикуляры MA'
, MB'
, MC'
на стороны. Найдите геометрическое место точек M
, для которых треугольник A'B'C'
— прямоугольный.
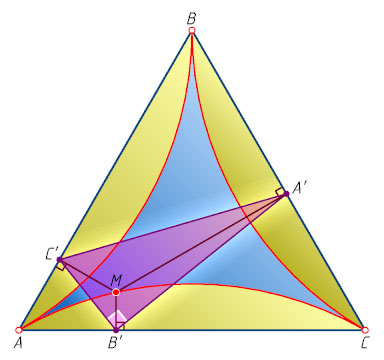
Ответ. Объединение трёх дуг, каждая из которых построена внутри треугольника на его стороне как на хорде и вмещает угол 150^{\circ}
(см. рис.).
Указание. Вычислите угол AMB
.
Решение. Пусть точки A'
, B'
и C'
лежат на сторонах BC
, AC
и AB
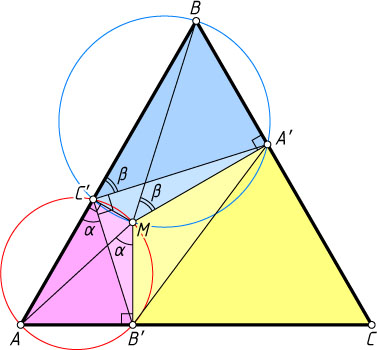
соответственно. Предположим, что \angle A'C'B'=90^{\circ}
(рис. 1).
Из точек A'
и C'
отрезок BM
виден под прямым углом. Значит, эти точки лежат на окружности с диаметром BM
. Аналогично точки A
, M
, B'
и C'
также лежат на одной окружности.
Обозначим
\angle B'C'A=\angle B'MA=\alpha,~\angle A'C'B=\angle A'MB=\beta.
Поскольку
\alpha+\beta=180^{\circ}-\angle A'C'B'=180^{\circ}-90^{\circ}=90^{\circ}~\mbox{и}
\angle A'MB'=180^{\circ}-\angle ACB=180^{\circ}-60^{\circ}=120^{\circ},
то
\angle AMB=360^{\circ}-(\alpha+\beta)-\angle A'MB'=360^{\circ}-90^{\circ}-120^{\circ}=150^{\circ}.
Из полученных равенств также следует, что если \angle AMB=150^{\circ}
, то
\angle A'C'B'=180^{\circ}-(\alpha+\beta)=180^{\circ}-(360^{\circ}-\angle AMB-\angle A'MB')=
=180^{\circ}-360^{\circ}+150^{\circ}+120^{\circ}=90^{\circ}.
Значит, множество точек M
, для которых \angle A'C'B'=90^{\circ}
, — есть дуга окружности, проходящей через точки A
и B
, вмещающая угол 150^{\circ}
.
Полным ответом (рис. 2) будет объединение трёх таких дуг, соответствующих случаям \angle A'=90^{\circ}
, \angle B'=90^{\circ}
, \angle C'=90^{\circ}
(см. задачу 10555).
Источник: Турнир городов. — 1986-1987, VIII, весенний тур, старшие классы, основной вариант
Источник: Журнал «Crux Mathematicorum». — 2003, № 2, задача 2, с. 95
Источник: Ирландские математические олимпиады. — 1997

