4323. В трапеции ABCD
известно, что AB
— основание, AC=BC
, H
— середина AB
. Пусть l
— прямая, проходящая через точку H
и пересекающая прямые AD
и BD
в точках P
и Q
соответственно. Докажите, что либо углы ACP
и QCB
равны, либо их сумма равна 180^{\circ}
.
Решение. Пусть M
и N
— точки пересечения прямых соответственно CP
и CQ
с прямой AB
, K
— точка пересечения прямых PQ
и CD
. Тогда
DC:AM=DP:AP=DK:AH,
DC:BN=DQ:BQ=DK:BH,
а так как AH=BH
, то DC:AM=DC:BN
. Следовательно, AM=BN
.
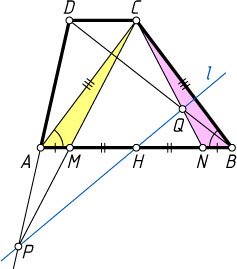
Рассмотрим случай, изображённый на рис. 1: точка P
лежит на продолжении стороны AD
за точку A
. Тогда точка Q
лежит на отрезке BD
(см. задачу 806), а точки M
и N
— на отрезке AB
. Треугольники ACM
и BCN
равны по двум сторонам (AC=BC
, AM=BN
) и углу между ними (\angle CAM=\angle CBN
как углы при основании равнобедренного треугольника ABC
), следовательно,
\angle ACP=\angle ACM=\angle BCN=\angle BCQ.
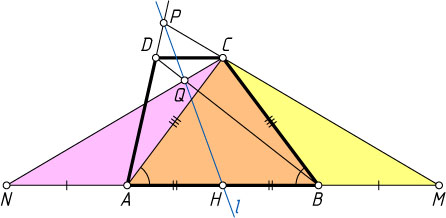
Пусть точка P
лежит на продолжении стороны AD
за точку D
(рис. 2). Тогда точка Q
лежит на отрезке BD
(см. задачу 806), точки M
и N
— на отрезке AB
. Треугольники ACM
и BCN
равны по двум сторонам (AC=BC
, AM=BN
) и углу между ними (\angle CAM=\angle CBN
как углы при основании равнобедренного треугольника ABC
), следовательно,
\angle ACP=180^{\circ}-\angle ACM=180^{\circ}-\angle BCN=180^{\circ}-\angle BCQ.
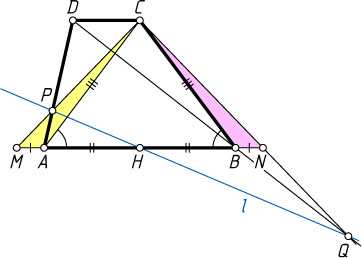
Если точка P
лежит на отрезке AD
, а точка Q
— на продолжении BD
за точку B
(рис. 3), то аналогично первому случаю \angle ACP=\angle BCQ
.
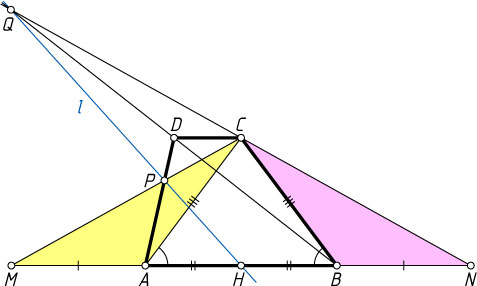
Если точка P
лежит на отрезке AD
, а точка Q
— на продолжении BD
за точку D
(рис. 4), то аналогично второму случаю \angle ACP=180^{\circ}-\angle BCQ
.
(Заметим, что во всех случаях обе точки M
и N
лежат либо внутри, либо вне отрезка AB
.)
Примечание. См. также решения «Задачника Кванта» (Квант, 1990, N12, с.23-24), где приведено решение с выходом в пространство.
Автор: Шарыгин И. Ф.
Источник: Турнир городов. — 1989-1990, XI, весенний тур, старшие классы, основной вариант
Источник: Журнал «Квант». — 1990, № 7, с. 30, М1233; 1990, № 12, с. 23, М1233
Источник: Задачник «Кванта». — М1233



