4352. Через вершину A
остроугольного треугольника ABC
проведены биссектрисы AM
и AN
внутреннего и внешнего углов и касательная AK
к описанной окружности треугольника ABC
(точки M
, K
, N
лежат на прямой BC
). Докажите, что MK=KN
.
Решение. Первый способ. Будем считать, что вершина C
лежит между точками M
и N
. Обозначим \angle BAC=\alpha
, \angle ABC=\beta
.
Из теоремы об угле между касательной и хордой следует, что
\angle KAC=\angle ABC=\beta.
Поскольку AMK
— внешний угол треугольника ABM
, а AM
— биссектриса угла A
, то
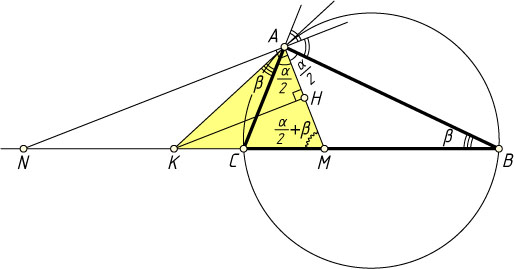
\angle AMK=\angle ABM+\angle MAB=\beta+\frac{\alpha}{2}=\angle KAC+\angle CAM=\angle KAM.
Значит, треугольник AKM
— равнобедренный. Его высота KH
является медианой, а так как AN\perp AM
(как биссектрисы смежных углов), то KH\parallel AN
. Следовательно, K
— середина MN
.
Второй способ. Заметим, что \angle MAN=90^{\circ}
как угол между биссектрисами смежных углов. Кроме того, AK=KN
(см. задачу 4708). Значит, точка K
лежит на серединном перпендикуляре к отрезку AN
, а так как этот серединный перпендикуляр параллелен AM
, то по теореме Фалеса K
— середина отрезка MN
.
Примечание. Из доказанного утверждения автоматически следует, что точка K
является центром окружности Аполлония треугольника ABC
.