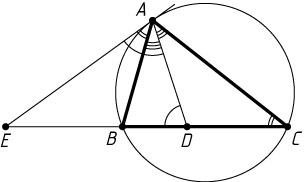
4708. Касательная в точке A
к описанной окружности треугольника ABC
пересекает прямую BC
в точке E
; AD
— биссектриса треугольника ABC
. Докажите, что AE=ED
.
Указание. Примените теорему об угле между касательной и хордой.
Решение. Пусть точка E
лежит на продолжении стороны BC
за точку B
. Применив теорему об угле между касательной и хордой и теорему о внешнем угле треугольника, получим, что
\angle EAD=\angle EAB+\angle BAD=\angle ACB+\angle DAC=\angle EDA.
Следовательно, треугольник ADE
— равнобедренный, и AE=ED
.
Примечание. Верно и обратное: если AE=ED
, то AD
— биссектриса треугольника ABC
(см. задачу 12503).
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.23, с. 33
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.25, с. 34
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 99
