4367. Вписанная окружность треугольника ABC
касается сторон AB
и AC
в точках P
и Q
соответственно. Пусть RS
— средняя линия треугольника, параллельная AB
, T
— точка пересечения прямых PQ
и RS
. Докажите, что T
лежит на биссектрисе угла B
треугольника.
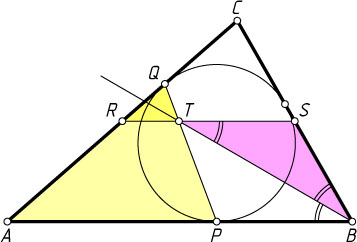
Решение. Первый способ. Пусть AB\gt BC
(случай AB\lt BC
разбирается аналогично). Будем считать, что R
лежит на AC
, S
— на BC
(рис. 1). Обозначим BC=a
, AC=b
, AB=c
, \frac{a+b+c}{2}=p
. Тогда
RQ=RC-QC=\frac{b}{2}-(p-c)=\frac{b}{2}-\frac{a+b-c}{2}=\frac{c-a}{2}.
Поскольку треугольники AQP
и RQT
подобны, а треугольник AQP
равнобедренный, то RQ=RT
. Следовательно,
ST=RS-RT=RS-RQ=\frac{c}{2}-\frac{c-a}{2}=\frac{a}{2}=BS.
Значит, треугольник TSB
— равнобедренный и
\angle SBT=\angle STB=\angle TBA.
Следовательно, BT
— биссектриса угла B
треугольника ABC
.
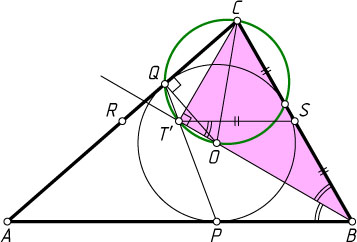
Второй способ. Пусть AB\gt BC
(случай AB\lt BC
разбирается аналогично). Будем считать, что R
лежит на AC
, S
— на BC
.
Пусть O
— центр вписанной окружности треугольника ABC
, T'
— точка пересечения биссектрисы угла ABC
с прямой PQ
(рис. 2). Обозначим углы треугольника ABC
через \alpha
, \beta
и \gamma
соответственно. Тогда
\angle OCQ=\frac{\gamma}{2},~\angle OT'Q=\angle BPT'+\angle PBT'=
=\left(90^{\circ}+\frac{\alpha}{2}\right)+\frac{\beta}{2}=90^{\circ}+\left(\frac{\alpha}{2}+\frac{\beta}{2}\right)=90^{\circ}+\left(90^{\circ}-\frac{\gamma}{2}\right)=180^{\circ}-\frac{\gamma}{2}.
Следовательно, точки O
, T'
, Q
и C
лежат на одной окружности, а так как \angle OQC=90^{\circ}
, то OC
— диаметр этой окружности. Значит, \angle BT'C=\angle OT'C=90^{\circ}
.
Поскольку T'S
— медиана прямоугольного треугольника BT'C
, проведённая из вершины прямого угла, то
\angle BT'S=\angle SBT'=\angle PBT'
(см. задачу 1109), поэтому ST'\parallel AB
. Следовательно, точка T'
лежит на средней линии SR
треугольника ABC
, а значит, совпадает с точкой T
.
