4711. Продолжения сторон AB
и CD
вписанного четырёхугольника ABCD
пересекаются в точке P
, а продолжения BC
и AD
— в точке Q
. Докажите, что точки пересечения биссектрис углов AQB
и BPC
со сторонами четырёхугольника являются вершинами ромба.
Указание. Если \cup AD\gt\cup BC
, то \angle APD=\frac{1}{2}(\cup AD-\cup BC)
.
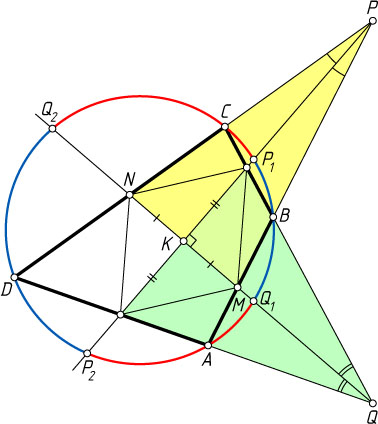
Решение. Пусть P_{1}
и P_{2}
— точки пересечения биссектрисы угла BPC
с окружностью, описанной около четырёхугольника ABCD
, а Q_{1}
и Q_{2}
— биссектрисы угла AQB
, причём точка P_{1}
лежит между P
и P_{2}
, Q_{1}
— между Q
и Q_{2}
. Тогда
\cup AP_{2}-\cup BP_{1}=\cup DP_{2}-\cup CP_{1},~\cup DQ_{2}-\cup AQ_{1}=\cup CQ_{2}-\cup BQ_{1},
или
\cup AP_{2}+\cup CP_{1}=\cup DP_{2}+\cup BP_{1},~\cup AQ_{1}+\cup CQ_{2}=\cup DQ_{2}+\cup BQ_{1}.
Сложив почленно эти два равенства, получим, что
\cup AP_{2}+\cup AQ_{1}+\cup CP_{1}+\cup CQ_{2}=\cup DP_{2}+\cup DQ_{2}+\cup BP_{1}+\cup BQ_{1}=180^{\circ}.
Если K
— точка пересечения указанных биссектрис, то
\angle PKQ=\angle P_{1}KQ_{1}=\frac{1}{2}(\cup AP_{2}+\cup AQ_{1}+\cup CP_{1}+\cup CQ_{2})=90^{\circ}
(см. задачу 26). Если M
и N
— точки пересечения прямой Q_{1}Q_{2}
со сторонами AB
и CD
, то треугольник PMN
— равнобедренный, так как его биссектриса PK
является высотой. Поэтому MK=KN
. Аналогично докажем, что K
— середина второй диагонали полученного четырёхугольника. Следовательно, это ромб.
Автор: Уртембаев М. К.
Источник: Журнал «Квант». — 1972, № 3, с. 39, М131; 1972, № 11, с. 45, M131
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.40, с. 35
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.43, с. 35
Источник: Хонсбергер Р. Математические изюминки. — М.: Наука, 1992. — № 330, с. 146
