4855. Из произвольной точки M
окружности, описанной около прямоугольника, опустили перпендикуляры MP
и MQ
на две его противоположные стороны, и перпендикуляры MR
и MT
— на продолжения двух других сторон. Докажите, что прямые PR
и QT
перпендикулярны друг другу, а их точка пересечения принадлежит диагонали прямоугольника.
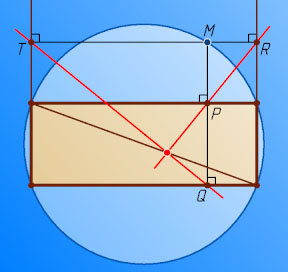
Указание. Пусть точки P
и Q
принадлежат сторонам AB
и CD
прямоугольника ABCD
, а точки T
и R
— продолжениям сторон AD
и BC
(рис. 1). Опишем окружность около прямоугольника APMT
. Пусть N
— точка пересечения отрезка TQ
с этой окружностью (отличная от T
). Докажите, что \angle APN=\angle RPB
.
Решение. Первый способ. Пусть точки P
и Q
принадлежат сторонам AB
и CD
прямоугольника ABCD
, а точки T
и R
— продолжениям сторон AD
и BC
(рис. 1). Опишем окружность около прямоугольника APMT
. Пусть N
— точка пересечения отрезка TQ
с этой окружностью (отличная от T
). Тогда
\angle APN=\angle ATN=\angle DTQ=\angle DMQ=\angle DMM_{1}=
=\frac{1}{2}\smile DM_{1}=\frac{1}{2}\smile AM=\angle MBA=\angle MBP=\angle RPB.
Поэтому точка N
лежит на прямой RP
, а так как \angle TNP=\angle TAP=90^{\circ}
, то PR\perp QT
.
Поскольку \angle QNR=\angle QCR=90^{\circ}
, точки N
, Q
, C
, R
лежат на одной окружности (рис. 2). Поэтому
\angle QNC=\angle QRC=\angle QMC=\angle M_{1}MC=
=\frac{1}{2}\smile M_{1}C=\frac{1}{2}\smile MB=\angle MAB=\angle APT=\angle ANT.
Следовательно, точка N
лежит на прямой AC
.
Второй способ (Квант, 1980, N1, с.33). Пусть точки P
и Q
принадлежат сторонам AB
и CD
прямоугольника ABCD
, а точки T
и R
— продолжениям сторон AD
и BC
(рис. 3). Четырёхугольник AM_{2}CM_{1}
— прямоугольник (все его углы — прямые, поскольку AC
и M_{1}M_{2}
— диаметры данной окружности), а четырёхугольники AM_{2}RP
и ATQM_{1}
— параллелограммы (поскольку M_{2}R=AP
, M_{2}R\parallel AP
и AT=M_{1}Q
, AT\parallel M_{1}Q
). Поэтому PR\parallel AM_{2}
и TQ\parallel AM_{1}
, а так как AM_{2}\perp AM_{1}
, то PR\perp TQ
.
Пусть N
— точка пересечения прямых PR
и TQ
. Докажем, что прямоугольники AFNG
и AM_{2}CM_{1}
подобны (отсюда будет следовать, что точка N
принадлежит диагонали AC
).
Обозначим
AM_{1}=a,~AM_{2}=b,~\angle ATF=\angle AM_{2}T=\angle MRP=\angle M_{2}CR=\alpha.
Тогда
AF=AT\sin\alpha=AM_{2}\sin^{2}\alpha=b\sin^{2}\alpha,
AG=M_{2}K=M_{2}R\sin\alpha=M_{2}C\sin^{2}\alpha=a\sin^{2}\alpha.
Поэтому \frac{AF}{AG}=\frac{b}{a}=\frac{AM_{2}}{AM_{1}}
. Следовательно, прямоугольники AFNG
и AM_{2}CM_{1}
подобны.
Третий способ. Лемма. Пусть стороны двух прямоугольников соответственно параллельны. В каждом из них проведём по одной диагонали. Тогда угол между этими диагоналями, равен углу между двумя другими.
Доказательство. Достаточно рассмотреть параллельный перенос, переводящий центр одного параллелограмма в центр другого, а затем симметрию относительно общего серединного перпендикуляра к параллельным сторонам прямоугольников.
Вернёмся к нашей задаче. Докажем перпендикулярность QT
и PR
. Из леммы следует, что угол между диагональю QT
прямоугольника DQMT
и диагональю PR
прямоугольника BRMP
равен углу между диагоналями MD
и BM
, т. е. углу BMD
. Точка M
лежит на окружности с диаметром BD
, значит, \angle BMD=90^{\circ}
.
Из задачи 3221 следует, что прямые PR
, QT
и AC
пересекаются в одной точке.
Примечание. См. статью В.Дубровского «Геометрические метаморфозы», Квант, 1997, N6, с.26-30.
Автор: Шафарян В.
Источник: Журнал «Квант». — 1979, № 2, с. 32, М546
Источник: Задачник «Кванта». — М546
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.65
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.66, с. 18
