4877. Прямая Штейнера. Докажите, что точки, симметричные относительно сторон треугольника, точке, лежащей на его описанной окружности, лежат на одной прямой, причём эта прямая проходит через точку пересечения высот треугольника.
Решение. Пусть D
— точка, лежащая на окружности, описанной около треугольника ABC
; A_{1}
, B_{1}
и C_{1}
— проекции точки D
на прямые BC
, AC
и AB
соответственно; A_{2}
, B_{2}
и C_{2}
— точки, симметричные точке D
относительно прямых соответственно BC
, AC
и AB
; H
— точка пересечения высот треугольника ABC
.
Заметим, что точки A_{1}
, B_{1}
и C_{1}
лежат на одной прямой — прямой Симсона треугольника ABC
, соответствующей точке D
(см. задачу 83). При гомотетии с центром D
и коэффициентом 2, точки A_{1}
, B_{1}
и C_{1}
переходят в точки соответственно A_{2}
, B_{2}
и C_{2}
. Следовательно, точки A_{2}
, B_{2}
и C_{2}
также лежат на одной прямой, причём эта прямая параллельна прямой Симсона, соответствующей точке D
.
Докажем, что эта прямая проходит через точку H
. Для этого достаточно доказать, что C_{2}H\parallel C_{1}A_{1}
.
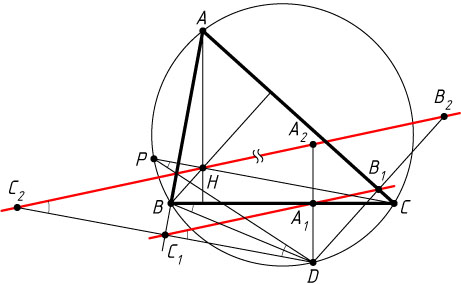
Рассмотрим случай, изображённый на рисунке. Пусть прямая CH
вторично пересекает окружность в точке P
. Тогда точка P
симметрична точке H
относительно прямой AB
, а значит, отрезки PD
и C_{2}H
симметричны относительно этой прямой. Кроме того, C_{2}D\parallel PH
, поэтому
\angle HC_{2}D=\angle PDC_{2}=\angle DPC=\angle DBC,
а так как из точек C_{1}
и A_{1}
отрезок BD
виден под прямым углом, то эти точки лежат на окружности с диаметром BD
. Значит,
\angle DBC=\angle DBA_{1}=\angle DC_{1}A_{1}.
Таким образом, \angle HC_{2}D=\angle DC_{1}A_{1}
. Следовательно, C_{2}H\parallel C_{1}A_{1}
. Что и требовалось доказать.
Аналогично для любого треугольника ABC
и любой точки D
, лежащей на его описанной окружности.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 63
