5045. С помощью циркуля и линейки постройте треугольник по точке H
пересечения его высот, центру O
описанной окружности и прямой l
, на которой лежит одна из его сторон.
Указание. Расстояние от точки пересечения высот до вершины треугольника вдвое больше расстояния от центра описанной окружности до противолежащей стороны (см. задачу 1257).
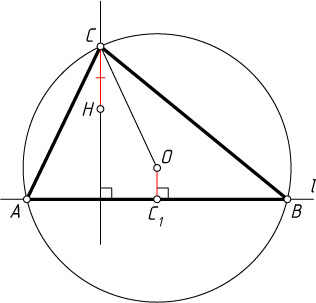
Решение. Предположим, что нужный треугольник ABC
построен. Пусть AB
— его сторона, лежащая на данной прямой l
, C_{1}
— середина этой стороны. Тогда CH=2OC_{1}
(см. задачу 1257).
Отсюда вытекает следующий способ построения. Строим проекцию C_{1}
точки O
на данную прямую l
. На прямой, проходящей через точку H
перпендикулярно прямой l
, откладываем отрезок HC
, равный 2OC_{1}
. Тогда C
— вершина искомого треугольника. Затем проводим окружность с центром O
и радиусом OC
. Её пересечение с прямой l
даёт вершины A
и B
искомого треугольника.
Источник: Васильев Н. Б. и др. Математические соревнования. Геометрия. — М.: Наука, 1974. — № 48, с. 11
