5047. Расстояние от точки пересечения высот треугольника ABC
до вершины C
равно стороне AB
. Найдите угол ACB
.
Ответ. 45^{\circ}
или 135^{\circ}
.
Указание. Расстояние от точки пересечения высот до вершины треугольника вдвое больше расстояния от центра описанной окружности до противолежащей стороны (см. задачу 1257).
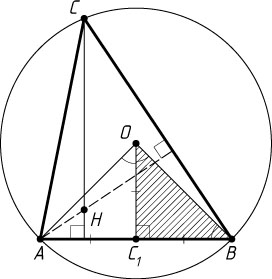
Решение. Первый способ. Пусть H
— точка пересечения высот треугольника ABC
, C_{1}
— середина стороны AB
, O
— центр описанной окружности. Поскольку CH=2OC_{1}
(см. задачу 1257), то
OC_{1}=\frac{1}{2}CH=\frac{1}{2}AB=C_{1}B.
Поэтому треугольник OC_{1}B
— прямоугольный и равнобедренный. Следовательно, \angle C_{1}OB=45^{\circ}
.
Если точки C
и O
лежат по одну сторону от прямой AB
, то
\angle C=\frac{1}{2}\angle AOB=\angle C_{1}OB=45^{\circ}.
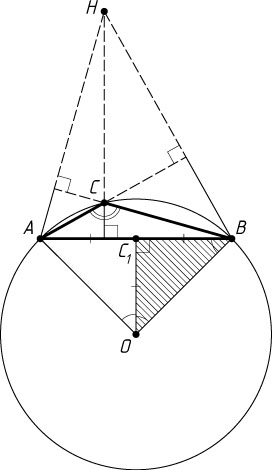
Если же точки C
и O
лежат по разные стороны от прямой AB
, то
\angle C=\frac{1}{2}(360^{\circ}-\angle AOB)=180^{\circ}-45^{\circ}=135^{\circ}.
Второй способ. Пусть H
— точка пересечения высот треугольника ABC
, C_{1}
— середина стороны AB
, O
— центр описанной окружности, R
— её радиус. Тогда AB^{2}=CH^{2}=4R^{2}-AB^{2}
(см. задачу 10768). Отсюда находим, что AB=R\sqrt{2}
.
По теореме синусов
\sin\angle C=\frac{AB}{2R}=\frac{R\sqrt{2}}{2R}=\frac{\sqrt{2}}{2}.
Следовательно, \angle C=45^{\circ}
или \angle C=135^{\circ}
.
Третий способ. Пусть H
— точка пересечения высот, а BK
— высота треугольника треугольника ABC
. Прямоугольные треугольники CKH
и AKB
равны по гипотенузе и острому углу, поэтому AKC
— равнобедренный прямоугольный треугольник. При этом угол ACK
(равный 45^{\circ}
) либо совпадает с углом ACB
, либо является смежным к нему.
Источник: Васильев Н. Б. и др. Математические соревнования. Геометрия. — М.: Наука, 1974. — № 51, с. 12
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.12, с. 123
Источник: Грибалко А. В., Медников Л. Э. XXI—XXII турниры математических боёв имени А. П. Савина. — М.: МЦНМО, 2020. — № 256, с. 35

