5210. Две окружности касаются внешним образом. A
— точка касания их общей внешней касательной с одной из окружностей, B
— точка той же окружности, диаметрально противоположная точке A
. Докажите, что длина касательной, проведённой из точки B
ко второй окружности, равна диаметру первой окружности.
Указание. Пусть C
— точка касания общей касательной со второй окружностью, H
— точка касания окружностей. Тогда точки B
, H
и C
лежат на одной прямой.
Решение. Пусть C
— точка касания общей касательной со второй окружностью, H
— точка касания окружностей, BD
— касательная ко второй окружности.
Через точку H
проведём общую касательную окружностей. Если M
— точка её пересечения с отрезком AC
, то AM=MH=MC
(равенство отрезков касательных, проведённых к окружности из одной точки). Медиана HM
треугольника AHC
равна половине стороны AC
, значит, \angle AHC=90^{\circ}
(см. задачу 1188).
Точка H
лежит на окружности с диаметром AB
, поэтому \angle AHB=90^{\circ}
. Следовательно, точки B
, H
и C
лежат на одной прямой.
По теореме о касательной и секущей BD^{2}=BC\cdot BH
. С другой стороны, AH
— высота прямоугольного треугольника ABC
, проведённая из вершины прямого угла, поэтому AB^{2}=BC\cdot BH
. Значит, BD^{2}=AB^{2}
, следовательно, BD=AB
. Что и требовалось доказать.
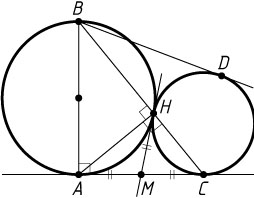
Источник: Журнал «Crux Mathematicorum». — 2011, № 3, задача 3, с. 158
Источник: Британская математическая олимпиада. — 2006-2007
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 791, с. 98
Источник: Всероссийская олимпиада школьников. — 2011-12 г., окружной тур, 11 кл.
