5307. В прямоугольном треугольнике ABC
проведена высота CH
из вершины прямого угла. Радиусы окружностей, вписанных в криволинейные треугольники AHC
, BHC
и ABC
, равны R_{1}
, R_{2}
и R_{3}
соответственно. Докажите, что R_{3}=R_{1}+R_{2}
.
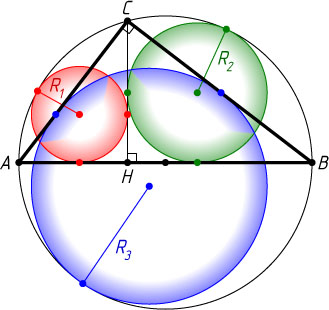
Решение. Пусть r
— радиус окружности, вписанной в треугольник ABC
. Тогда R_{3}=2r
(см. задачу 5104) и R_{1}+R_{2}=2r
(см. задачу 5093). Следовательно, R_{3}=R_{1}+R_{2}
.
Автор: Белосевич В. В.
