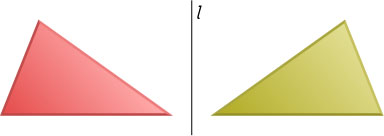
5404. На рисунке показаны равные симметричные относительно прямой l
треугольники. Разрежьте левый из них на части, из которых можно сложить правый, если части разрешается только сдвигать и поворачивать, но не переворачивать.
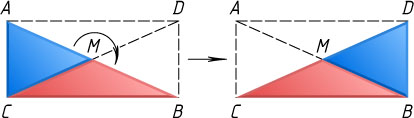
Решение. Пусть левый треугольник ABC
— прямоугольный с прямым углом при вершине C
(рис. 1). На продолжении его медианы CM
отложим отрезок MD
, равный CM
. Тогда ADBC
— прямоугольник, а прямоугольный треугольник DCB
равен треугольнику ABC
.
В этом случае разрез нужно провести по медиане CM
, а затем повернуть на 180^{\circ}
вокруг точки M
равнобедренный треугольник AMC
.
Основание H
высоты, проведённой из вершины наибольшего угла треугольника, лежит на стороне треугольника, а не на её продолжении (см. задачу 127).
Если левый треугольник не прямоугольный (рис. 2), то разрезав его на два прямоугольных по высоте, проведённой из вершины наибольшего угла, сведём этот случай к разобранному.
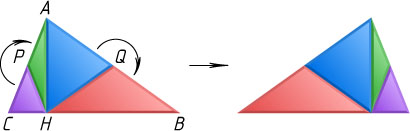
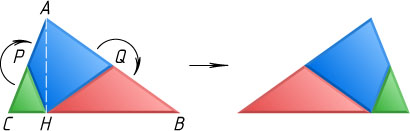
Примечание. Во второй части можно обойтись только двумя разрезами: по медианам HP
и HQ
треугольников, примыкающих к высоте (разрез по высоте — лишний).
Источник: Тригг Ч. Задачи с изюминкой. — М.: Мир, 1975. — № 204, с. 48



