5413. Различные точки A
, B
, C
и D
лежат на одной прямой. Постройте квадрат, две стороны которого лежат на параллельных прямых, проходящих через точки A
и B
, а две другие — на параллельных прямых, проходящих через C
и D
.
Решение. Без ограничения общности будем считать, что точки A
, B
, C
и D
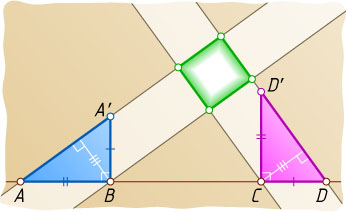
лежат на одной прямой в указанном порядке (см. рис.).
Через точки B
и C
проведём прямые, перпендикулярные прямой AB
, и отложим в одной из полуплоскостей с границей AB
отрезки BA'=CD
и CD'=AB
. Затем через точку B
проведём прямую, параллельную прямой AA'
, а через точку C
— прямую, параллельную прямой DD'
. Докажем, что пересечения пар построенных параллельных прямых — вершины искомого квадрата.
Действительно, прямоугольные треугольники ABA'
и D'CD
равны по двум катетам, поэтому равны их гипотенузы AA'=DD'
, углы BAA'
и CDD'
в сумме дают 90^{\circ}
, а также равны высоты этих треугольников, проведённые из вершин прямых углов, т. е. (см. задачу 1967). Значит, в пересечении получился прямоугольник, стороны которого равны этим высотам. Следовательно, это квадрат. Что и требовалось доказать.
Аналогично для случаев, когда пары параллельных проводятся через A
и C
, B
и D
; и A
и D
, B
и C
. Кроме того, нужно добавить случаи, симметричные отмеченным относительно прямой AD
. Таким образом, задача имеет 3+3=6
решений.
Источник: Журнал «Crux Mathematicorum». — 1976, № 6, задача 127 (1976, 41), с. 124
