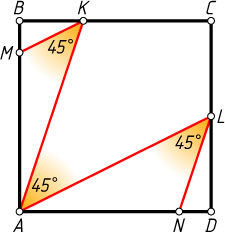
5458. В квадрат ABCD
вписана ломаная MKALN
, причём \angle MKA=\angle KAL=\angle ALN=45^{\circ}
(см. рис.). Докажите, что MK^{2}+AL^{2}=AK^{2}+NL^{2}
.
Указание. Точка, симметричная точке B
относительно прямой AK
, совпадает с точкой, симметричной точке D
относительно прямой AL
.
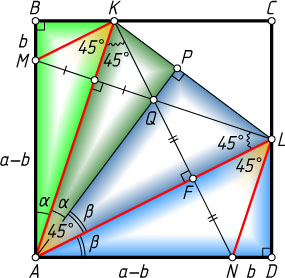
Решение. Обозначим \angle BAK=\alpha
, \angle DAL=\beta
. Тогда \alpha+\beta=45^{\circ}
.
Пусть при симметрии относительно прямой AK
точка B
перейдёт в P
, а точка M
— в точку Q
. Тогда AP=AB=AD
, \angle PAK=\alpha
и \angle APK=90^{\circ}
. Значит,
\angle PAL=\angle KAL-\angle PAK=45^{\circ}-\alpha=\beta,
и при симметрии относительно прямой AL
луч AD
перейдёт в луч AP
, а так как AP=AD
, то точка D
при этом перейдёт в точку P
, а прямоугольный треугольник ADL
— в прямоугольный треугольник APL
. Следовательно, точка P
лежит на отрезке KL
.
Пусть прямая KQ
пересекает AL
в точке F
. Из треугольника AKF
находим, что
\angle AFK=180^{\circ}-\angle KAL-\angle AKF=
=180^{\circ}-\angle KAL-\angle AKQ=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}.
Значит, KQ\perp AL
, следовательно, Q
— точка пересечения высот треугольника KAL
, и LQ\perp AK
. Это означает, что при симметрии относительно прямой AL
точка N
перейдёт в Q
. Таким образом AN=AQ=AM
и DN=BM
.
Обозначим AB=a
, DN=BM=b
. По теореме Пифагора
BK^{2}=AK^{2}-AB^{2}=AK^{2}-a^{2},~BK^{2}=MK^{2}-BM^{2}=MK^{2}-b^{2},~
DL^{2}=AL^{2}-AD^{2}=AL^{2}-a^{2},~DL^{2}=NL^{2}-DN^{2}=NL^{2}-b^{2}.
Из равенств
AK^{2}-a^{2}=MK^{2}-b^{2},~AL^{2}-a^{2}=NL^{2}-b^{2}
следует, что MK^{2}+AL^{2}=AK^{2}+NL^{2}
. Что и требовалось доказать.
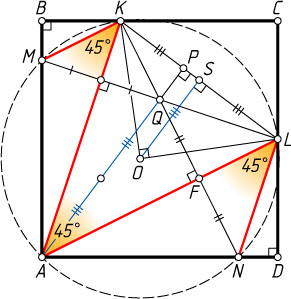
Примечание. Кроме того AM=AN=AQ=KL
, а точки M
, K
, A
, L
, N
лежат на одной окружности.
Пусть O
— центр описанной окружности треугольника AKL
, S
— середина KL
. Тогда AQ=2OS
(см. задачу 1257), а так как \angle KOL=2\angle KAL=90^{\circ}
, то OS=\frac{1}{2}KL
. Следовательно, AQ=2OS=KL
.
Поскольку MK\parallel AL
(накрест лежащие углы равны) и AM=KL
, четырёхугольник AMKL
— равнобедренная трапеция, значит, около неё можно описать окружность. Поэтому точки A
, M
, K
и L
лежат на одной окружности — окружности, описанной около треугольника AKL
. Аналогично на этой окружности лежит и точка N
.
