5759. Найдите стороны параллелограмма ABCD
, в котором радиусы окружностей, описанных около треугольников ABC
и ABD
, равны 5 и \sqrt{13}
соответственно, а расстояние между центрами этих окружностей равно 2.
Ответ. AB=6
, AD=9\sqrt{\frac{2}{5}}
.
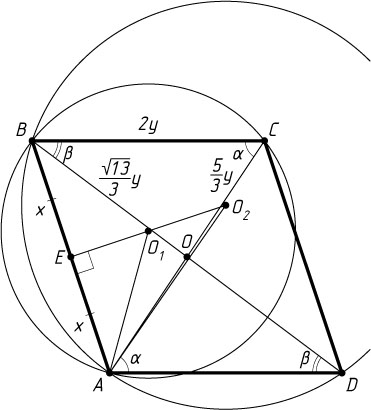
Решение. Пусть O
— центр параллелограмма ABCD
, O_{1}
и O_{2}
— центры описанных окружностей треугольников ABC
и ABD
соответственно, а прямая O_{1}O_{2}
пересекает отрезок AB
в точке E
. Поскольку AB
— общая хорда окружностей, точка E
— середина AB
и O_{1}O_{2}\perp AB
.
Пусть AB=2x
, BC=2y
, \angle ACB=\angle CAD=\alpha
, \angle ADB=\angle DBC=\beta
. Тогда AO_{1}=5
, AO_{2}=\sqrt{13}
, AE=BE=x
. Из прямоугольных треугольников AO_{1}E
и AO_{2}E
находим, что O_{1}E=\sqrt{25-x^{2}}
и O_{2}E=\sqrt{13-x^{2}}
. Поскольку O_{1}O_{2}=O_{1}E-O_{2}E
, получим уравнение
\sqrt{25-x^{2}}-\sqrt{13-x^{2}}=2,
из которого находим, что x=3
. Следовательно, AB=2x=6
.
По теореме синусов из треугольников ABC
и ABD
находим, что
\sin\alpha=\frac{AB}{2\cdot5}=\frac{3}{5},~\sin\beta=\frac{AB}{2\cdot\sqrt{13}}=\frac{3}{\sqrt{13}}.
Тогда \cos\alpha=\frac{4}{5}
, \cos\beta=\frac{2}{\sqrt{13}}
,
\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta=\frac{3}{5}\cdot\frac{2}{\sqrt{13}}+\frac{4}{5}\cdot\frac{3}{\sqrt{13}}=\frac{18}{5\sqrt{13}}.
По теореме синусов из треугольника BOC
находим, что
BO=BC\cdot\frac{\sin\alpha}{\sin(\alpha+\beta)}=\frac{2y\cdot\frac{3}{5}}{\frac{18}{5\sqrt{13}}}=\frac{\sqrt{13}}{3}y,~CO=BC\cdot\frac{\sin\beta}{\sin(\alpha+\beta)}=\frac{2y\cdot\frac{3}{\sqrt{13}}}{\frac{18}{5\sqrt{13}}}=\frac{5}{3}y,
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон (см. задачу 4011), т. е. (2BO)^{2}+(2CO)^{2}=2AB^{2}+2BC^{2}
, или
4\left(\frac{\sqrt{13}}{3}y\right)^{2}+4\left(\frac{5}{3}y\right)^{2}=2\cdot36+2\cdot4y^{2},
откуда y^{2}=\frac{81}{10}
. Следовательно,
BC=2y=\frac{18}{\sqrt{10}}=9\sqrt{\frac{2}{5}}.
Источник: Вступительный экзамен в МФТИ. — 2005, билет 5, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 05-5-4, с. 440
