5763. В треугольнике ABC
проведены биссектрисы AE
и CD
. Найдите длины отрезков CD
, CE
, DE
и расстояние между центрами окружностей, вписанной в треугольник ABC
и описанной около треугольника ABC
, если AC=2
, BC=4
, \angle ACB=\arccos\frac{11}{16}
.
Ответ. CD=\sqrt{6}
, CE=\frac{8}{5}
, DE=\frac{\sqrt{34}}{5}
, \rho=2\sqrt{\frac{2}{5}}
.
Решение. Обозначим \angle ACB=\gamma
, \angle ABC=\beta
. По условию задачи \cos\gamma=\frac{11}{16}
. Тогда
\sin\gamma=\sqrt{1-\cos^{2}\gamma}=\sqrt{1-\frac{121}{256}}=\frac{3\sqrt{15}}{16}.
По теореме косинусов
AB=\sqrt{AC^{2}+BC^{2}-2AC\cdot BC\cos\gamma}=\sqrt{4+16-2\cdot2\cdot4\cdot\frac{11}{16}}=\sqrt{20-11}=3.
По свойству биссектрисы треугольника
\frac{AD}{DB}=\frac{AC}{BC}=\frac{2}{4}=\frac{1}{2},~\frac{CE}{BE}=\frac{AC}{AB}=\frac{2}{3},
поэтому
AD=\frac{1}{3}AB=1,~BD=\frac{2}{3}AB=2,~CE=\frac{2}{5}BC=\frac{2}{5}\cdot4=\frac{8}{5},~BE=\frac{12}{5}.
По формуле для биссектрисы треугольника (см. задачу 791)
CD=\sqrt{AC\cdot BC-AD\cdot BD}=\sqrt{2\cdot4-1\cdot2}=\sqrt{6}.
Пусть R
— радиус описанной окружности треугольника ABC
, O
— центр этой окружности. По теореме синусов
R=\frac{AB}{2\sin\gamma}=\frac{3}{2\cdot\frac{3\sqrt{15}}{16}}=\frac{8}{\sqrt{15}},~\sin\beta=\frac{AC}{2R}=\frac{2}{2\cdot\frac{8}{\sqrt{15}}}=\frac{\sqrt{15}}{8}.
Тогда \cos\beta=\frac{7}{8}
. Из треугольника BDE
по теореме косинусов находим, что
DE=\sqrt{BD^{2}+BE^{2}-2BD\cdot BE\cos\beta}=\sqrt{4+\frac{144}{25}-2\cdot2\cdot\frac{12}{5}\cdot\frac{7}{8}}=\frac{\sqrt{34}}{5}.
Пусть r
— радиус вписанной окружности треугольника ABC
, p
— полупериметр треугольника, S
— площадь. Тогда
p=\frac{2+3+4}{2}=\frac{9}{2},~S=\frac{1}{2}AC\cdot BC\sin\gamma=\frac{1}{2}\cdot2\cdot4\cdot\frac{3\sqrt{15}}{16}=\frac{3\sqrt{15}}{4}.
Следовательно,
r=\frac{S}{p}=\frac{\frac{3\sqrt{15}}{4}}{\frac{9}{2}}=\frac{\sqrt{15}}{6}.
Пусть вписанная окружность с центром Q
касается стороны AC
треугольника ABC
в точке M
, а N
— середина этой стороны. Тогда
CM=p-AB=\frac{9}{2}-3=\frac{3}{2},~MN=|CM-CN|=\frac{3}{2}-1=\frac{1}{2}.
По теореме Пифагора
ON=\sqrt{OC^{2}-CN^{2}}=\sqrt{R^{2}-CN^{2}}=\sqrt{\frac{64}{15}-1}=\frac{7}{\sqrt{15}}.
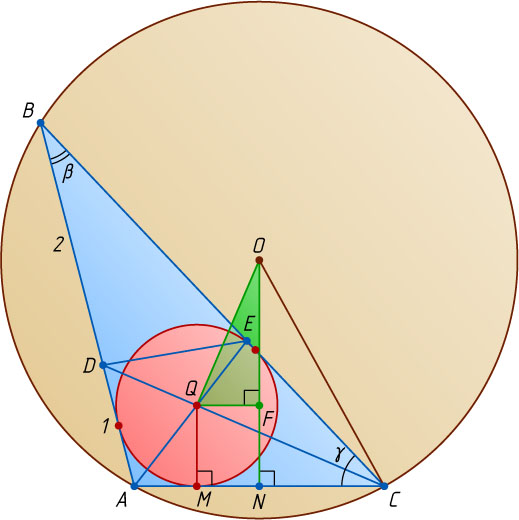
Искомый отрезок OQ
есть большая боковая сторона прямоугольной трапеции MNOQ
с основаниями MQ
и ON
. Пусть F
— основание перпендикуляра, опущенного из точки Q
на ON
. Тогда
OF=|ON-FN|=|ON-QM|=\left|\frac{7}{\sqrt{15}}-\frac{5}{2\sqrt{15}}\right|=\frac{9}{2\sqrt{15}},
QF=MN=|CN-CM|=\left|1-\frac{3}{2}\right|=\frac{1}{2}.
Следовательно,
\rho=OQ=\sqrt{QF^{2}+OF^{2}}=\sqrt{\frac{1}{4}+\frac{27}{20}}=2\sqrt{\frac{2}{5}}.
Примечание. Для нахождения расстояния между центрами вписанной и описанной окружностей треугольника можно воспользоваться формулой Эйлера (см. задачу 126):
\rho=\sqrt{R^{2}-2Rr}.
Источник: Вступительный экзамен в МФТИ. — 2005, билет 9, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 05-9-3, с. 443
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.22, с. 40
