5939. Стороны треугольника относятся как 2:3:3
.
а) Докажите, что точки касания вписанной и вневписанной окружностей треугольника делят его большую сторону на три равных отрезка.
б) Найдите отношение радиусов этих окружностей.
Ответ. 1:4
.
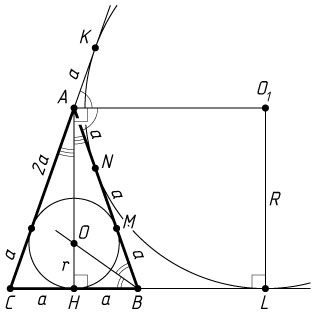
Решение. а) Пусть AB=AC=3a
, BC=2a
— стороны треугольника ABC
, p=\frac{1}{2}(2a+3a+3a)=4a
— его полупериметр, M
и N
— точки касания соответственно вписанной и вневписанной окружностей со стороной AB
, K
— точка касания вневписанной окружности с продолжением стороны AC
, H
— точка касания вписанной окружности со стороной BC
. Поскольку треугольник равнобедренный, H
— середина основания BC
.
Тогда
BM=BH=a,~AN=AK=CK-AC=p-3a=4a-3a=a
(см. задачу 4805), значит,
MN=AB-BM-AN=3a-a-a=a.
Следовательно, BM=MN=AN
.
б) Пусть O
и O_{1}
— центры соответственно вписанной и вневписанной окружностей треугольника ABC
, r
и R
— их радиусы, L
— точка касания вневписанной окружности с продолжением основания BC
. Тогда
\angle AHL=\angle HLO_{1}=90^{\circ},
а так как центр окружности, вписанной в угол, лежит на его биссектрисе, то AO_{1}
и AH
— биссектрисы смежных углов, значит, \angle HAO_{1}=90^{\circ}
. Тогда AHLO_{1}
— прямоугольник, поэтому AH=O_{1}L=R
.
По свойству биссектрисы треугольника
\frac{OH}{OA}=\frac{BH}{BA}=\frac{a}{3a}=\frac{1}{3}.
Следовательно,
\frac{r}{R}=\frac{OH}{AH}=\frac{OH}{OH+OA}=\frac{1}{4}.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.51.1, с. 120
