6011. Точки M
и N
лежат на сторонах соответственно AC
и AB
треугольника ABC
(или на их продолжениях). На отрезках BM
и CN
как на диаметрах построены окружности. Докажите что их радикальная ось проходит через ортоцентр треугольника ABC
.
Указание. Если BB_{1}
и CC_{1}
— высоты треугольника ABC
, а H
— его ортоцентр, то BH\cdot HB_{1}=CH\cdot HC_{1}
.
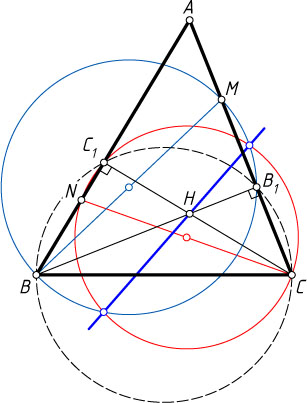
Решение. Пусть BB_{1}
и CC_{1}
— высоты треугольника ABC
. Из точки B_{1}
отрезок BM
виден под прямым углом, поэтому точка B_{1}
лежит на окружности с диаметром BM
. Аналогично точка C_{1}
лежит на окружности с диаметром CN
.
Пусть H
— ортоцентр треугольника ABC
. Поскольку точки B
, C
, B_{1}
и C_{1}
лежат на одной окружности, BH\cdot HB_{1}=CH\cdot HC_{1}
, т. е. степени точки H
относительно окружностей с диаметрами BM
и CN
равны. Следовательно, точка H
лежит на радикальной оси этих окружностей (см. задачу 6391).
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 51
