6038. Круг разделили хордой AB
на два круговых сегмента и один из них повернули на некоторый угол вокруг точки A
. Пусть при этом повороте точка B
перешла в точку D
(см.рис.). Докажите, что отрезки, соединяющие середины дуг сегментов с серединой отрезка BD
, перпендикулярны друг другу.
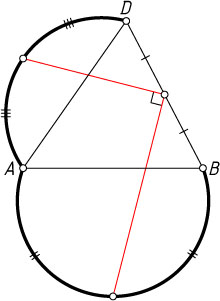
Указание. Рассмотрите композицию двух поворотов: вокруг точки C
на угол BCA
и вокруг точки E
на угол AED
, где C
и E
— середины дуг AB
и AD
соответственно.
Решение. Первый способ. Пусть C
и E
— середины дуг соответственно оставшейся на месте дуги AB
и дуги AD
, M
— середина отрезка BD
(рис. 1).
Рассмотрим композицию поворота вокруг точки C
, переводящего точку B
в A
, и поворота вокруг точки E
, переводящего A
в D
(оба поворота против часовой стрелки). Поскольку \angle BCA+\angle AED=180^{\circ}
, эта композиция есть центральная симметрия (см. задачу 6710). Центр симметрии — середина отрезка между точкой B
и её образом D
при рассматриваемой композиции, т. е. точка M
.
Образ C_{1}
точки C
при этой композиции лежит на продолжении отрезка CM
за точку M
(C_{1}M=MC
). С другой стороны, при первом повороте точка C
остаётся на месте, а при втором — переходит в точку C_{1}
. Поэтому EC_{1}=EC
. Значит, ME
— медиана, а следовательно, высота равнобедренного треугольника CEC_{1}
, т. е. EM\perp MC
.
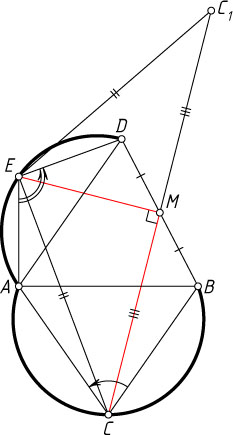
Второй способ. Пусть C
и E
— середины дуг соответственно оставшейся на месте дуги AB
и дуги AD
, M
— середина отрезка BD
(рис. 2), K
и H
— середины отрезков AD
и AB
соответственно, F
— диаметрально противоположна точке C
(середина «старой» дуги AB
).
HM
и KM
— средние линии равнобедренного треугольника ABD
, поэтому AKMH
— ромб. Следовательно, EK\perp AD
, AD\parallel HM
, CH\perp AB
, AB\parallel KM
и \angle EKM=\angle MHC
как углы с соответственно перпендикулярными сторонами.
Кроме того,
CH:HM=CH:AH=AH:HF=AK:KE=MK:KE,
значит, треугольники CHM
и MKE
подобны, а так как у них две пары сторон соответственно перпендикулярны, то и третья тоже: EM\perp MC
.
Автор: Насыров З.
Источник: Турнир городов. — 1991-1992, XII, весенний тур, младшие классы, основной вариант
Источник: Журнал «Квант». — 1992, № 2, с. 20, М1327
Источник: Задачник «Кванта». — М1327

