6092. Докажите, что проекция стороны AB
треугольника ABC
на прямую Симсона, соответствующую точке M
, равна расстоянию между проекциями точки M
на прямые AC
и BC
.
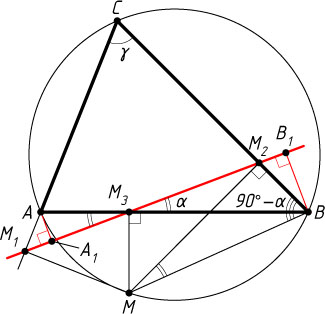
Решение. Рассмотрим случай, изображённый на рисунке. Пусть M
— точка, лежащая на описанной окружности треугольника ABC
и отличная от вершин треугольника, M_{1}
, M_{2}
и M_{3}
— проекции точки M
, на прямые AC
, BC
и AB
соответственно, A_{1}
и B_{1}
— проекции точек A
и B
на прямую M_{1}M_{2}
(прямую Симсона, соответствующую точке M
, см. задачу 83).
Обозначим \angle ACB=\gamma
, \angle AM_{3}M_{1}=\angle BM_{3}M_{2}=\alpha
, R
— радиус описанной окружности треугольника ABC
. Тогда
AB=2R\sin\gamma,~CM=2R\sin\angle CBM,~A_{1}B_{1}=AB\cos\alpha=2R\sin\gamma\cos\alpha.
Из точек M_{1}
и M_{2}
отрезок CM
виден под прямым углом, значит, эти точки лежат на окружности с диаметром CM
. Поэтому
M_{1}M_{2}=CM\sin\gamma=2R\sin\angle CBM\sin\gamma.
Из точек M_{2}
и M_{3}
отрезок MB
виден под прямым углом, значит, эти точки лежат на окружности с диаметром MB
. Тогда
\angle BMM_{2}=\angle BM_{3}M_{2}=\alpha,~\angle CBM=90^{\circ}-\alpha,
поэтому
M_{1}M_{2}=2R\sin\angle CBM\sin\gamma=2R\sin(90^{\circ}-\alpha)\sin\gamma=2R\cos\alpha\sin\gamma.
Следовательно, M_{1}M_{2}=A_{1}B_{1}
. Что и требовалось доказать.
Аналогично для остальных случаев.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 453, с. 54
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.90, с. 116
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.110, с. 114
