6125. Теорема Морлея. Докажите, что точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника.
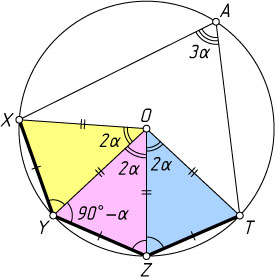
Решение. Первый способ. (Доказательство М.Т.Нераньенгара, 1909 г.) Докажем сначала следующую лемму. Если четыре точки X
, Y
, Z
и T
таковы, что XY=YZ=ZT
и \angle XYZ=\angle YZT=180^{\circ}-2\alpha\gt60^{\circ}
, то они лежат на одной окружности. Кроме того, если точки A
и Y
лежат по разные стороны от прямой XT
и при этом \angle XAT=3\alpha
, то точка A
также лежит на этой окружности.
Доказательство. Пусть O
— точка пересечения биссектрис углов XYZ
и YZT
(рис. 1). Тогда треугольник OXY
равен равнобедренному треугольнику OZY
по двум сторонам и углу между ними. Аналогично, треугольник OZT
также равен треугольнику OZY
, значит, OT=OX=OY=OZ
. Следовательно, точки X
, Y
, Z
и T
лежат на окружности с центром O
.
Угол при вершине каждого из трёх отмеченных равнобедренных треугольников равен 180^{\circ}-2(90^{\circ}-\alpha)=2\alpha
, значит, дуга XYZT
полученной окружности равна 6\alpha
, а так как \angle XAT=3\alpha
, то точка A
лежит на этой окружности. Лемма доказана.
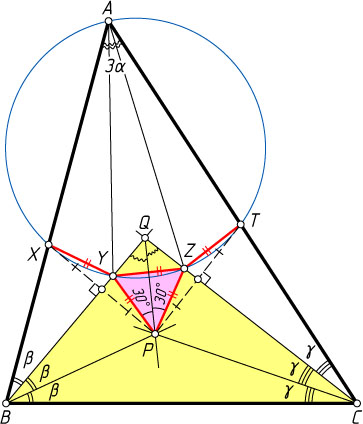
Рассмотрим произвольный треугольник ABC
с углами, равными 3\alpha
, 3\beta
и 3\gamma
соответственно (рис. 2). Пусть смежные трисектрисы углов при вершинах B
и C
пересекаются в точке P
, а две другие трисектрисы этих углов — в точке Q
. Тогда P
— точка пересечения биссектрис треугольника BQC
, поэтому QP
— биссектриса угла BQC
. Кроме того,
\angle BPQ=90^{\circ}+\frac{1}{2}\angle BCQ=90^{\circ}+\frac{1}{2}\cdot2\gamma=90^{\circ}+\gamma
(см. задачу 1101).
Отметим на сторонах QB
и QC
треугольника BQC
точки соответственно Y
и Z
, для которых \angle QPY=\angle QPZ=30^{\circ}
. Тогда
\angle BPY=\angle BPQ-\angle YPQ=90^{\circ}+\gamma-30^{\circ}=60^{\circ}+\gamma.
Треугольники QPY
и QPZ
равны по стороне и двум прилежащим к ней углам, поэтому PY=PZ
, а так как \angle YPZ=60^{\circ}
, то треугольник PYZ
— равносторонний.
Пусть X
— точка, симметричная точке P
относительно биссектрисы BQ
угла ABP
, а T
— точка, симметричная точке P
относительно биссектрисы CQ
угла ACP
. Тогда
XY=YZ=YP=ZP=ZT,~\angle BXY=\angle BPY=60^{\circ}+\gamma,
\angle XYP=360^{\circ}-\angle PBX-2\angle BPY=360^{\circ}-2\beta-120^{\circ}-2\gamma=
=240^{\circ}-2(\beta+\gamma)=240^{\circ}-2(60^{\circ}-\alpha)=120^{\circ}+2\alpha,
\angle XYZ=360^{\circ}-\angle XYP-\angle PYZ=360^{\circ}-(120^{\circ}+2\alpha)-60^{\circ}=180^{\circ}-2\alpha.
Аналогично, \angle YZT=180^{\circ}-2\alpha
. Заметим, что \alpha\lt60^{\circ}
, так как 3\alpha\lt180^{\circ}
, поэтому
180^{\circ}-2\alpha\gt180^{\circ}-120^{\circ}=60^{\circ}.
Значит, для точек X
, Y
, Z
, T
и A
выполнены все условия леммы. Следовательно, эти пять точек лежат на одной окружности, поэтому вписанные углы XAY
, YAZ
и ZAT
, опирающиеся на равные хорды XY
, YZ
и ZT
, равны, т. е. AY
и AZ
— трисектрисы угла BAC
.
Второй способ. Пусть углы треугольника ABC
равны 3\alpha
, 3\beta
и 3\gamma
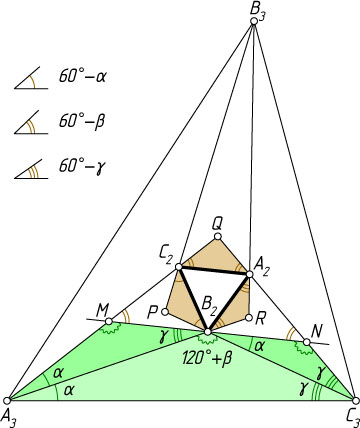
соответственно. Рассмотрим равносторонний треугольник A_{2}B_{2}C_{2}
. На его сторонах построим вне его как на основаниях равнобедренные треугольники A_{2}B_{2}R
, B_{2}C_{2}P
и C_{2}A_{2}Q
с углами соответственно 60^{\circ}-\gamma
, 60^{\circ}-\alpha
и 60^{\circ}-\beta
при основаниях (рис. 3).
Лучи RB_{2}
и QC_{2}
пересекаются в некоторой точке A_{3}
, причём точки A_{3}
и A_{2}
лежат по разные стороны от прямой B_{2}C_{2}
, так как
\angle RB_{2}C_{2}+\angle QC_{2}B_{2}=(60^{\circ}-\gamma+60^{\circ})+(60^{\circ}-\beta+60^{\circ})=240^{\circ}-\beta-\gamma=
=180^{\circ}+60^{\circ}-\beta-\gamma=180^{\circ}+\alpha\gt180^{\circ}.
Аналогично, лучи RA_{2}
и PC_{2}
пересекаются в некоторой точке B_{3}
, а лучи PB_{2}
и QA_{2}
— в некоторой точке C_{3}
, причём точки B_{3}
и B_{2}
лежат по разные стороны от прямой A_{2}C_{2}
, а точки C_{3}
и C_{2}
— по разные стороны от прямой A_{2}B_{2}
.
Докажем, что лучи A_{3}B_{2}
, A_{3}C_{2}
, B_{3}C_{2}
, B_{3}A_{2}
, C_{3}A_{2}
и C_{3}B_{2}
— трисектрисы углов треугольника A_{3}B_{3}C_{3}
.
Через точку B_{2}
проведём прямую, параллельную A_{2}C_{2}
. Пусть эта прямая пересекает лучи QA_{3}
и QC_{3}
в точках M
и N
соответственно. Треугольники B_{2}C_{2}M
и B_{2}A_{2}N
равны по стороне и двум прилежащим к ней углам, поэтому B_{2}M=B_{2}N
, т. е. B_{2}
— середина отрезка MN
.
Вычислим углы треугольников A_{3}MB_{2}
и B_{2}NC_{3}
.
\angle NB_{2}C_{3}=\angle MB_{2}P=\angle MB_{2}C_{2}-\angle PB_{2}C_{2}=\angle A_{2}B_{2}C_{2}-\angle PB_{2}C_{2}=60^{\circ}-(60^{\circ}-\alpha)=\alpha.
Аналогично, \angle MB_{2}A_{3}=\gamma
. Углы B_{2}NC_{3}
и \angle B_{2}MA_{3}
равны как внешние углы при основании равнобедренного треугольника QMN
, причём
\angle B_{2}NC_{3}=\angle B_{2}MA_{3}=180^{\circ}-\angle B_{2}MC_{2}=180^{\circ}-\angle A_{2}C_{2}Q=180^{\circ}-(60^{\circ}-\beta)=120^{\circ}+\beta.
\angle NC_{3}B_{2}=180^{\circ}-\angle NB_{2}C_{3}-\angle B_{2}NC_{3}=180^{\circ}-\alpha-(120^{\circ}+\beta)=60^{\circ}-\alpha-\beta=\gamma.
Значит, треугольники A_{3}MB_{2}
и B_{2}NC_{3}
подобны. Поэтому \frac{B_{2}C_{3}}{B_{2}A_{3}}=\frac{B_{2}N}{A_{3}M}=\frac{B_{2}M}{A_{3}M}
, а так как
\angle A_{3}B_{2}C_{3}=180^{\circ}-\angle NB_{2}C_{3}-\angle MB_{2}A_{3}=180^{\circ}-\alpha-\gamma=120^{\circ}+(60^{\circ}-\alpha-\gamma)=120^{\circ}+\beta=\angle B_{2}MA_{3},
то треугольники A_{3}B_{2}C_{3}
и A_{3}MB_{2}
также подобны, поэтому
\angle B_{2}A_{3}C_{3}=\angle MA_{3}B_{2}=\alpha,~\angle B_{2}C_{3}A_{3}=\angle MB_{2}A_{3}=\gamma.
Аналогично, \angle A_{2}C_{3}B_{3}=\gamma
. Следовательно, лучи C_{3}B_{2}
и C_{3}A_{2}
— трисектрисы угла A_{3}C_{3}B_{3}
. Аналогично докажем, что лучи A_{3}B_{2}
и A_{3}C_{2}
— трисектрисы угла B_{3}A_{3}C_{3}
, а лучи B_{3}A_{2}
и B_{3}C_{2}
— трисектрисы угла A_{3}B_{3}C_{3}
.
Таким образом, точки пересечения смежных трисектрис треугольника A_{3}B_{3}C_{3}
— вершины равностороннего треугольника. Следовательно, точки пересечения смежных трисектрис подобного ему треугольника ABC
— также вершины равностороннего треугольника. Что и требовалось доказать.
Третий способ. Пусть смежные трисектрисы углов A
и C
треугольника ABC
пересекаются в точке Y
, смежные трисектрисы углов B
и C
— в точке X
, углов A
и B
— в точке Z
. Пусть углы треугольника ABC
равны 3\alpha
, 3\beta
и 3\gamma
соответственно, BC=a
, AC=b
и AB=c
, CX=m
и CY=n
, а радиус описанной окружности треугольника ABC
равен R
.
Тогда, так как \alpha+\beta+\gamma=60^{\circ}
, то
\angle AYC=180^{\circ}-(\alpha+\gamma)=180^{\circ}-(60^{\circ}-\beta)=120^{\circ}+\beta.
По теореме синусов
\frac{CY}{\sin\angle CAY}=\frac{AC}{\sin\angle AYC},~\mbox{или}~\frac{n}{\sin\alpha}=\frac{b}{\sin(120^{\circ}+\beta)},
откуда n=\frac{b\sin\alpha}{\sin(120^{\circ}+\beta)}
, а так как
b=AC=2R\sin\angle ABC=2R\sin3\beta,
то
n=\frac{b\sin\alpha}{\sin(120^{\circ}+\beta)}=\frac{2R\sin3\beta\sin\alpha}{\sin(120^{\circ}+\beta)}=\frac{2R\sin3\beta\sin\alpha}{\sin(60^{\circ}-\beta)}.
Применяя известные формулы тригонометрии, получим, что
\sin3\beta=3\sin\beta-4\sin^{3}\beta=4\sin\beta\left(\frac{3}{4}-\sin^{2}\beta\right)=
=4\sin\beta\left(\left(\frac{\sqrt{3}}{2}\right)^{2}-\sin^{2}\beta\right)=4\sin\beta(\sin^{2}60^{\circ}-\sin^{2}\beta)=
=4\sin\beta(\sin60^{\circ}-\sin\beta)(\sin60^{\circ}+\sin\beta)=
=4\sin\beta\cdot2\sin\frac{60^{\circ}-\beta}{2}\cos\frac{60^{\circ}+\beta}{2}\cdot2\sin\frac{60^{\circ}+\beta}{2}\cos\frac{60^{\circ}-\beta}{2}=
=4\sin\beta\cdot2\sin\frac{60^{\circ}-\beta}{2}\cos\frac{60^{\circ}-\beta}{2}\cdot2\sin\frac{60^{\circ}+\beta}{2}\cos\frac{60^{\circ}+\beta}{2}=
=4\sin\beta\sin(60^{\circ}-\beta)\sin(60^{\circ}+\beta).
Значит,
\frac{2R\sin3\beta\sin\alpha}{\sin(60^{\circ}-\beta)}=\frac{2R\cdot4\sin\beta\sin(60^{\circ}-\beta)\sin(60^{\circ}+\beta)\cdot\sin\alpha}{\sin(60^{\circ}-\beta)}=
=8R\sin(60^{\circ}+\beta)\sin\alpha\sin\beta.
Аналогично,
m=8R\sin(60^{\circ}+\alpha)\sin\alpha\sin\beta.
По теореме косинусов из треугольника CXY
получаем, что
z^{2}=XY^{2}=m^{2}+n^{2}-2mn\cos\gamma=
=64R^{2}\sin^{2}(60^{\circ}+\alpha)\sin^{2}\alpha\sin^{2}\beta+64R^{2}\sin^{2}(60^{\circ}+\beta)\sin^{2}\alpha\sin\beta-
-2\cdot64R^{2}\sin^{2}\alpha\sin^{2}\beta\sin(60^{\circ}+\alpha)\sin(60^{\circ}+\beta)\cos\gamma=
=64R^{2}\sin^{2}\alpha\sin^{2}\beta(\sin^{2}(60^{\circ}+\alpha)+\sin^{2}(60^{\circ}+\beta)-2\sin(60^{\circ}+\alpha)\sin(60^{\circ}+\beta)\cos\gamma).
Заметим, что
(60^{\circ}+\alpha)+(60^{\circ}+\beta)+\gamma=120^{\circ}+\alpha+\beta+\gamma=120^{\circ}+60^{\circ}=180^{\circ},
поэтому существует треугольник EFG
с углами
\angle E=60^{\circ}+\alpha,~\angle F=60^{\circ}+\beta,~\angle G=\gamma.
Пусть R_{1}=\frac{1}{2}
— радиус описанной окружности этого треугольника. По теореме синусов
e0=FG=2R_{1}\sin(60^{\circ}+\alpha)=\sin(60^{\circ}+\alpha),
f=EG=2R_{1}\sin(60^{\circ}+\beta)=\sin(60^{\circ}+\beta),~g=EF=2R\sin\gamma=\sin\gamma.
Применяя к треугольнику EFG
теорему косинусов, получим, что
\sin^{2}(60^{\circ}+\alpha)+\sin^{2}(60^{\circ}+\beta)-2\sin(60^{\circ}+\alpha)\sin(60^{\circ}+\beta)\cos\gamma=
=e^{2}+f^{2}-ef\cos\gamma=g^{2}=\sin^{2}\gamma.
Значит,
z^{2}=64R^{2}\sin^{2}\alpha\sin^{2}\beta(\sin^{2}(60^{\circ}+\alpha)+\sin^{2}(60^{\circ}+\beta)-2\sin(60^{\circ}+\alpha)\sin(60^{\circ}+\beta)\cos\gamma)=
=64R^{2}\sin^{2}\alpha\sin^{2}\beta\sin^{2}\gamma,
откуда
XY=z=8R\sin\alpha\sin\beta\sin\gamma.
Аналогично,
YZ=x=8R\sin\alpha\sin\beta\sin\gamma~\mbox{и}~XZ=y=8R\sin\alpha\sin\beta\sin\gamma.
Следовательно, треугольник XYZ
равносторонний.
Четвёртый способ (Л.Штейнгарц). Пусть ABC
— данный треугольник, а треугольник XYZ
образован трисектрисами углов данного треугольника (рис. 4). Докажем, что треугольник XYZ
равносторонний.
Введём обозначения: \angle A=3\alpha
, \angle B=3\beta
, \angle C=3\gamma
. Рассмотрим произвольный равносторонний треугольник A_{1}B_{1}C_{1}
(рис. 5). Построим на стороне B_{1}C_{1}
такой треугольник B_{1}C_{1}A_{2}
, что \angle C_{1}B_{1}A_{2}=\gamma+60^{\circ}
и B_{1}C_{1}A_{2}=\beta+60^{\circ}
. Тогда
\angle B_{1}A_{2}C_{1}=180^{\circ}-(\gamma+60^{\circ})-(\beta+60^{\circ})=60^{\circ}-\gamma-\beta=\alpha,
так как \alpha+\beta+\gamma=60^{\circ}
.
Точно так же построим ещё два треугольника A_{1}C_{1}B_{2}
и A_{1}B_{1}C_{2}
. Лучи A_{2}B_{1}
и B_{2}A_{1}
пересекутся в некоторой точке M
, так как сумма углов B_{1}A_{2}B_{2}
и A_{1}B_{2}A_{2}
меньше 180^{\circ}
. При этом для треугольника A_{2}MB_{2}
выполняются условия задачи 10849. Поэтому A_{2}C_{1}
будет биссектрисой угла B_{1}A_{2}B_{2}
, а B_{2}C_{1}
— биссектрисой угла A_{1}B_{2}A_{2}
. Это означает, что
\angle C_{1}A_{2}B_{2}=\alpha,~\angle C_{1}B_{2}A_{2}=\beta.
Аналогичный результат получается и в остальных случаях (для A_{2}B_{1}
, C_{2}B_{1}
, C_{2}A_{1}
и B_{2}A_{1}
). Таким образом, оказывается, что в треугольнике A_{2}B_{2}C_{2}
проведены трисектрисы, и они при своём пересечении определяют равносторонний треугольник. Но очевидно, что треугольники A_{2}B_{2}C_{2}
и ABC
подобны (по углам). Следовательно, и треугольник XYZ
также равносторонний. Теорема доказана.
Примечание. См. также статью Г.Тонояна и И.Яглома «Теорема Морлея», Квант, 1978, N8, с.28-32.
Источник: Журнал «Crux Mathematicorum». — 1977, № 10, с. 276-296
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 97, с. 31
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — с. 44
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 61
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.56, с. 111
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.64, с. 108
Источник: Факультативный курс по математике: Учебное пособие для 7—9 кл. средней школы / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — с. 338
Источник: Журнал «Квант». — 1978, № 8, с. 30