6127. Докажите что из двух неравных хорд окружности большая удалена от центра на меньшее расстояние. Верно ли обратное?
Ответ. Верно.
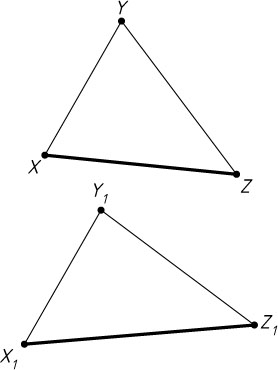
Решение. Воспользуемся следующей леммой (рис. 1). Если стороны XY
и XZ
треугольника XYZ
соответственно равны сторонам X_{1}Y_{1}
и X_{1}Z_{1}
треугольника X_{1}Y_{1}Z_{1}
, а YZ\gt Y_{1}Z_{1}
, то \angle YXZ\gt\angle Y_{1}X_{1}Z_{1}
. Обратно, если XY=X_{1}Y_{1}
и XZ=X_{1}Z_{1}
, а \angle YXZ\gt\angle Y_{1}X_{1}Z_{1}
, то YZ\gt Y_{1}Z_{1}
(см. задачу 3606).
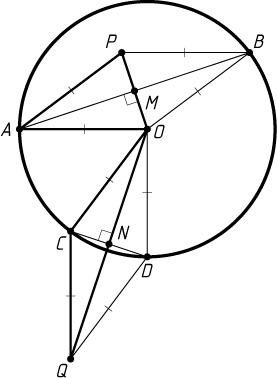
Пусть AB
и CD
— отличные от диаметра хорды окружности с центром O
(рис. 2), причём AB\gt CD
, M
и N
соответственно — проекции центра окружности на эти хорды. Тогда OM
и ON
— высоты равнобедренных треугольников AOB
и COD
с равными боковыми сторонами OA=OB=OC=OD
и неравными основаниями AB\gt AC
. Докажем, что высота OM
треугольника AOB
с большим основанием AB
, меньше высоты ON
треугольника COD
.
Действительно, по лемме \angle AOB\gt\angle COD
, поэтому \angle OAB\lt\angle OCD
. На продолжении отрезка OM
за точку M
отложим отрезок MP
, равный OM
, а на продолжении отрезка ON
за точку N
— отрезок NQ
, равный ON
. Рассмотрим равнобедренные треугольники OAP
и OCQ
. Известно, что AP=AO=CO=CQ
и \angle OAP\lt\angle OCQ
, поэтому OP\lt OQ
. Следовательно, OM=\frac{1}{2}OP\lt\frac{1}{2}CQ=ON
. Что и требовалось доказать.
Аналогично можно доказать и обратное, т. е. если расстояние от центра окружности до хорды AB
меньше расстояния от центра окружности до хорды CD
, то AB\gt CD
.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 71

