6149. Продолжения противоположных сторон AB
и CD
четырёхугольника ABCD
пересекаются в точке P
, а продолжения сторон BC
и AD
— в точке Q
. Докажите, что середины диагоналей AC
и BD
, а также середина отрезка PQ
лежат на одной прямой (прямая Гаусса).
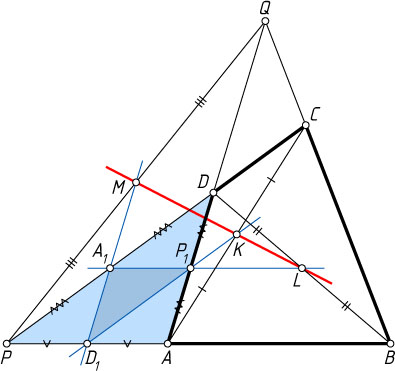
Решение. Первый способ. Пусть K
, L
и M
— середины AC
, BD
и PQ
соответственно (рис. 1), а точки P_{1}
, A_{1}
и D_{1}
— середины сторон соответственно AD
, DP
и AP
треугольника APD
. Тогда точки D_{1}
, K
и P_{1}
лежат на одной прямой — средней линии треугольника APD
. Аналогично, точки A_{1}
, L
, P_{1}
лежат на одной прямой и точки D_{1}
, M
, A_{1}
лежат на одной прямой.
Применив теорему Менелая (см. задачу 1622) к треугольнику APD
и прямой BQ
, получим, что
\frac{PB}{BA}\cdot\frac{AQ}{QD}\cdot\frac{DC}{CP}=1,
а так как
\frac{PB}{BA}=\frac{A_{1}L}{LP_{1}},~\frac{DC}{CP}=\frac{P_{1}K}{KD_{1}},~\frac{AQ}{QD}=\frac{D_{1}M}{MA_{1}},
то
\frac{A_{1}L}{LP_{1}}\cdot\frac{P_{1}K}{KD_{1}}\cdot\frac{D_{1}M}{MA_{1}}=\frac{PB}{BA}\cdot\frac{DC}{CP}\cdot\frac{AQ}{QD}=1.
Следовательно, по теореме, обратной теореме Менелая (треугольник A_{1}D_{1}P_{1}
), точки K
, L
и M
лежат на одной прямой.
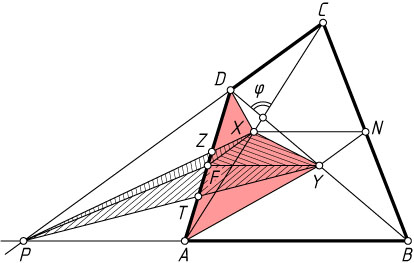
Второй способ (для выпуклого четырёхугольника). Лемма. Если X
и Y
— середины диагоналей соответственно AC
и BD
выпуклого четырёхугольника ABCD
(рис. 2), а прямые AB
и CD
пересекаются в точке P
, то площадь треугольника PXY
в четыре раза меньше площади четырёхугольника ABCD
.
Пусть F
— середина стороны AD
, а точка P
и сторона BC
лежат по разные стороны от прямой AD
. Отрезок FX
— средняя линия треугольника ACD
, поэтому FX\parallel CP
. Аналогично FY\parallel BP
. Точка Z
пересечения диагоналей DF
и PX
трапеции DPFX
лежит внутри трапеции DPFX
, а точка T
пересечения диагоналей трапеции APFY
— внутри трапеции APFY
, поэтому точка F
лежит на отрезке ZT
, а значит, внутри треугольника PXY
.
Треугольник PFX
равновелик треугольнику DFX
, а треугольник PFY
— треугольнику AFY
, значит, треугольник PXY
равновелик четырёхугольнику ADXY
, диагонали AX
и DY
которого равны половинам диагоналей AC
и BD
четырёхугольника ABCD
. Поскольку площадь любого четырёхугольника равна половине произведения диагоналей на синус угла \varphi
между ними, то
S_{\triangle PXY}=S_{ADXY}=\frac{1}{2}AX\cdot DY\sin\varphi=\frac{1}{2}\cdot\frac{1}{2}AC\cdot\frac{1}{2}BD\sin\varphi=
=\frac{1}{4}\cdot\frac{1}{2}AC\cdot BD\sin\varphi=\frac{1}{4}S_{ABCD}.
Лемма доказана.
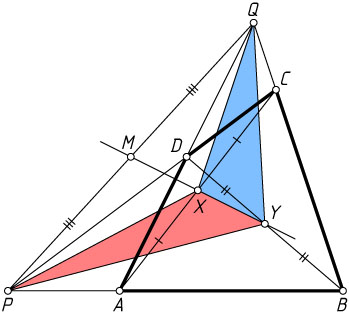
Заметим, что аналогично площадь треугольника QXY
также равна четверти площади четырёхугольника ABCD
(рис. 3), поэтому треугольники PXY
и QXY
равновелики, а так как XY
— их общая сторона, то точки P
и Q
, лежащие по разные стороны от прямой XY
, равноудалены от этой прямой. Значит, прямая XY
проходит через середину отрезка PQ
. Отсюда следует утверждение задачи.
