6164. Прямая, перпендикулярная гипотенузе прямоугольного треугольника с катетами 6 и 8, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите площадь этого четырёхугольника.
Ответ. 18 или 21\frac{1}{3}
.
Решение. Заметим, что окружность, вписанная в четырёхугольник, о котором говорится в условии задачи, — это окружность вписанная в данный прямоугольный треугольник.
Пусть вписанная окружность прямоугольного треугольника ABC
касается катета AC=8
в точке D
, катета BC=6
— в точке E
, а гипотенузы AB=10
— в точке F
. Пусть O
— центр этой окружности, r
— её радиус. Тогда
r=\frac{AC+BC-AB}{2}=\frac{8+6-10}{2}=2
(см. задачу 217).
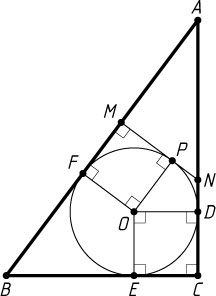
Предположим, что прямая, проходящая через точку M
, лежащую на гипотенузе, перпендикулярна гипотенузе, касается окружности в точке P
и пересекает катет AC
в точке N
(рис. 1). Четырёхугольники ODCE
и OFMP
— квадраты со стороной r=2
, поэтому
FM=OP=2,~CE=OD=2,~BE=BC-CE=6-2=4,
BF=BE=4,~BM=BF+FM=4+2=6,~AM=AB-BM=10-6=4.
Прямоугольный треугольник ANM
подобен треугольнику ABC
по двум углам, причём коэффициент подобия равен \frac{AM}{AC}=\frac{4}{8}=\frac{1}{2}
, значит,
S_{\triangle ANM}=\frac{1}{4}S_{\triangle ABC}=\frac{1}{4}\cdot\frac{1}{2}BC\cdot AC=\frac{1}{4}\cdot\frac{1}{2}\cdot6\cdot8=6.
Следовательно,
S_{BMNC}=S_{\triangle ABC}-S_{\triangle ANM}=24-6=18.
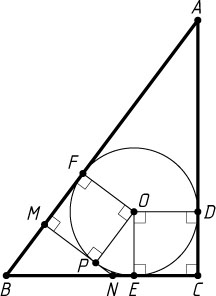
Пусть теперь прямая, проходящая через точку M
, лежащую на гипотенузе, перпендикулярна гипотенузе, касается окружности в точке P
и пересекает катет BC
в точке N
(рис. 2). Тогда
AD=AC-CD=8-2=6,~BM=AB-AM=AB-(AF+FM)=10-(6+2)=2,
треугольник NBM
подобен треугольнику ABC
по двум углам, причём коэффициент подобия равен \frac{BM}{BC}=\frac{2}{6}=\frac{1}{3}
, значит,
S_{\triangle NBM}=\frac{1}{9}S_{\triangle ABC}=\frac{1}{9}\cdot24=\frac{8}{3}.
Следовательно,
S_{AMNC}=S_{\triangle ABC}-S_{\triangle NBM}=24-\frac{8}{3}=\frac{64}{3}=21\frac{1}{3}.
Источник: ЕГЭ. — Задача C4, 2011

