6176. Высота равнобедренного треугольника, опущенная на основание, равна 45, точка касания вписанной окружности с боковой стороной делит эту сторону в отношении 8:9
, считая от основания. Найдите радиус окружности, касающейся стороны треугольника и продолжений двух других его сторон.
Ответ. 40
или 45
.
Решение. Первый способ. Пусть AD
— высота равнобедренного треугольника ABC
, опущенная на его основание BC
, O
— центр вписанной окружности, P
— точка её касания с боковой стороной AB
. Положим AP=9x
, BP=8x
. Тогда AB=AP+BP=17x
, BD=BP=8x
.
По теореме Пифагора AB^{2}-BD^{2}=AD^{2}
, или
(17x)^{2}-(8x)^{2}=45^{2},~9\cdot25x^{2}=9^{2}\cdot5^{2},
откуда x=3
. Значит,
AP=9x=27,~BD=8x=24,~AB=17x=51.
Обозначим \angle BAD=\alpha
. Из прямоугольного треугольника ABD
находим, что \tg\alpha=\frac{BD}{AD}=\frac{24}{45}=\frac{8}{15}
.
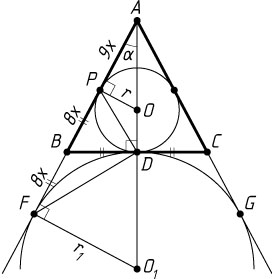
Пусть окружность с центром O_{1}
и радиусом r_{1}
касается продолжений боковых сторон AB
и AC
в точках F
и G
соответственно (рис. 1), а также основания BC
. Тогда D
— точка касания, поэтому
BF=BD=24,~AF=AB+BF=AB+BD=51+24=75.
Следовательно,
r_{1}=O_{1}F=AF\tg\alpha=75\cdot\frac{8}{15}=40.
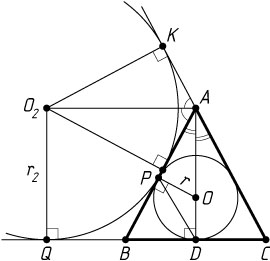
Пусть теперь окружность с центром O_{2}
радиуса r_{2}
касается боковой стороны AB
, продолжения основания BC
в точке Q
и продолжения боковой стороны AC
в точке K
(рис. 2). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому AO_{2}
и AD
— биссектрисы смежных углов BAK
и DAB
, значит, \angle DAO_{2}=90^{\circ}
. Тогда ADQO_{2}
— прямоугольник. Следовательно, r_{2}=O_{2}Q=AD=45
.
Радиус окружности, касающейся боковой стороны AC
и продолжений основания BC
и боковой стороны AB
, также равен 45.
Второй способ. Пусть S
— площадь треугольника ABC
, p
— его полупериметр. Тогда
S=\frac{1}{2}BC\cdot AD=\frac{1}{2}\cdot48\cdot45=1080,
r_{1}=\frac{S}{p-BC}=\frac{1080}{75-48}=\frac{1080}{27}=40,
r_{2}=\frac{S}{p-AB}=\frac{1080}{75-51}=\frac{1080}{24}=45
(см. задачу 392).
