6216. Пусть A
и B
— точки, лежащие на окружности. Они разбивают окружность на две дуги. Найдите геометрическое место середин всевозможных хорд, концы которых лежат на разных дугах AB
.
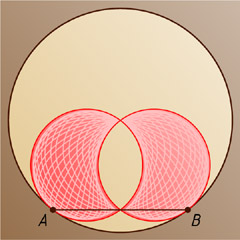
Ответ. Искомое ГМТ состоит из точек, лежащих внутри ровно одного из двух кругов с диаметрами OA
и OB
(см.рис. 1).
Решение. Воспользуемся следующими очевидными утверждениями:
1) отрезок, соединяющий центр окружности с серединой хорды (не являющейся диаметром), перпендикулярен этой хорде;
2) концы хорды лежат на разных дугах AB
тогда и только тогда, когда хорда пересекает отрезок AB
(во внутренней точке).
Тогда задачу можно переформулировать так: даны точки A
, B
и O
, причём OA=OB
; требуется найти геометрическое место таких точек M
, что прямая, проходящая через точку M
перпендикулярно OM
, пересекает отрезок AB
.
Докажем следующее утверждение: перпендикуляр l
к отрезку MO
пересекает отрезок AB
тогда и только тогда, когда ровно один из углов OMA
и OMB
— тупой.
Действительно, перпендикуляр l
пересекает отрезок AB
тогда и только тогда, когда точки A
и B
лежат в разных плоскостях относительно этого перпендикуляра. Пусть, например, точка B
лежит в той же полуплоскости, что и точка O
(рис. 2), а точка A
— в другой полуплоскости. \angle AMO\gt90^{\circ}
, а \angle BMO\lt90^{\circ}
. Если A
и O
лежат в одной полуплоскости относительно l
, а B
— в другой, то угол AMO
— острый, а BMO
— тупой. Если все точки лежат в одной полуплоскости, то оба угла острые. Если точки A
и B
лежат в одной полуплоскости, а точка O
— в другой, то оба угла — тупые. Таким образом, разобраны все возможные случаи, так что утверждение доказано.
Геометрическое место точек M
, из которых отрезок OA
виден под тупым углом, есть внутренность круга с диаметром OA
(см. задачу 1772), а ГМТ точек M
, из которых отрезок OB
виден под тупым углом, есть внутренность круга с диаметром OB
. Значит, искомое ГМТ состоит из точек, лежащих внутри ровно одного из двух кругов с диаметрами OA
и OB
. Следовательно, это ГМТ представляет собой внутренность этих кругов, за исключением их общей части (рис. 1).
 <
<
Автор: Шарыгин И. Ф.
Источник: Московская математическая олимпиада. — 1996, LIX, 9 класс
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2005, I, финальный тур, задача 3, 9 класс
Источник: Журнал «Квант». — 1996, № 4, с. 27, М1557
Источник: Задачник «Кванта». — М1557
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 5, с. 30
 <
<
