6296. Одна из вневписанных окружностей треугольника ABC
касается стороны AB
и продолжений сторон CA
и CB
в точках C_{1}
, B_{1}
и A_{1}
соответственно. Другая вневписанная окружность касается стороны AC
и продолжений сторон BA
и BC
в точках B_{2}
, C_{2}
и A_{2}
соответственно. Прямые A_{1}B_{1}
и A_{2}B_{2}
пересекаются в точке P
, прямые A_{1}C_{1}
и A_{2}C_{2}
— в точке Q
. Докажите, что точки A
, P
и Q
лежат на одной прямой.
Решение. Утверждение 1. Середина D
отрезка A_{1}A_{2}
является также серединой стороны BC
.
Доказательство. Обозначим AB=c
, BC=a
, AC=b
. Известно, что BA_{2}=CA_{1}=p
, где p
— полупериметр треугольника. Тогда, если D
— середина A_{1}A_{2}
, то
DA_{1}=\frac{1}{2}A_{1}A_{2}=\frac{1}{2}(A_{1}B+BC+CA_{2})=\frac{1}{2}((p-a)+a+(p-a))=
=\frac{1}{2}(2p-a)=\frac{1}{2}(b+c+a-a)=\frac{b+c}{2}.
Значит,
BD=DA_{1}-BA_{1}=\frac{b+c}{2}-(p-a)=\frac{b+c}{2}-\frac{b+c-a}{2}=\frac{a}{2},
т. е. D
— середина BC
. Утверждение 1 доказано.
Утверждение 2. Луч AP
— биссектриса угла BAB_{1}
.
Доказательство. Заметим, что прямая PA_{2}
параллельна биссектрисе угла при вершине C
треугольника ABC
(биссектриса внешнего угла равнобедренного треугольника A_{2}CB_{2}
параллельна основанию A_{2}B_{2}
). В то же время, биссектриса угла ACB
перпендикулярна прямой A_{1}B_{1}
(в равнобедренном треугольнике A_{1}CB_{1}
биссектриса угла при вершине является высотой). Значит, \angle A_{1}PA_{2}=90^{\circ}
. Поэтому PD
— медиана прямоугольного треугольника A_{1}PA_{2}
, проведённая из вершины прямого угла. Следовательно (см. задачу 1109),
\angle DA_{2}P=\angle DPA_{2},~\angle A_{1}DP=2\angle DA_{2}P=\angle ACB,
поэтому DP\parallel AC
, а так как D
— середина стороны BC
, то прямая DP
содержит среднюю линию треугольника ABC
, а значит, проходит через середину E
стороны AB
. Тогда
EP=PD-ED=DA_{2}-ED=\frac{b+c}{2}-\frac{b}{2}=\frac{c}{2}=AE,
т. е. треугольник PEA
— равнобедренный, а так как EP\parallel CB_{1}
, то
\angle EAB_{1}=180^{\circ}-\angle AEP=180^{\circ}-(180^{\circ}-2\angle EAP)=2\angle EAP.
Следовательно, AP
— биссектриса угла BAB_{1}
. Утверждение 2 доказано.
Перейдём к нашей задаче. Аналогично докажем, что луч AQ
— биссектриса угла CAC_{2}
. Поскольку биссектрисы вертикальных углов являются дополнительными лучами, точки A
, P
и Q
лежат на одной прямой.
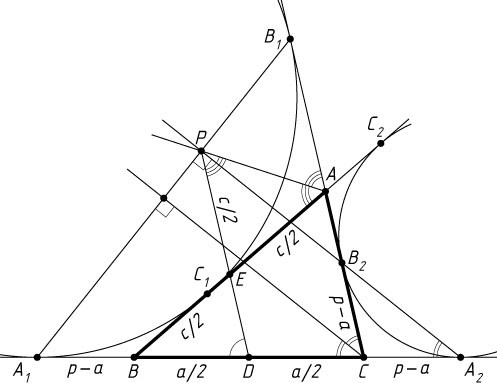
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2000 г., второй тур, 10 класс
