6424. На каждой из сторон треугольника ABC
построено по прямоугольнику так, что они попарно касаются вершинами (см. рис.). Докажите, что прямые, соединяющие вершины треугольника ABC
с соответствующими вершинами треугольника A_{1}B_{1}C_{1}
, пересекаются в одной точке.
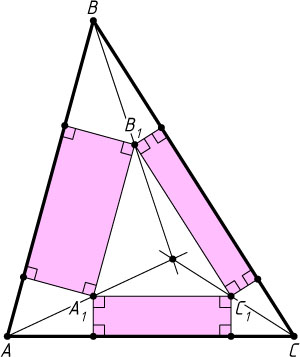
Указание. Примените гомотетию.
Решение. У треугольников ABC
и A_{1}B_{1}C_{1}
попарно параллельные стороны, следовательно, они гомотетичны. Прямые, соединяющие их соответствующие вершины пересекаются в одной точке (см. задачу 5000).
Источник: Журнал «Квант». — 1982, № 5, с. 29, задача 4
