6430. Поризм Штейнера. Докажите, что если существует цепочка окружностей S_{1}
, S_{2}
, \dots
, S_{n}
, каждая из которых касается двух соседних (S_{n}
касается S_{n-1}
и S_{1}
) и двух данных непересекающихся окружностей R_{1}
и R_{2}
, то таких цепочек бесконечно много. А именно, для любой окружности T_{1}
, касающейся R_{1}
и R_{2}
(одинаковым образом, если R_{1}
и R_{2}
не лежат одна внутри другой, внешним и внутренним в противном случае), существует аналогичная цепочка из n
касающихся окружностей T_{1}
, T_{2}
, …, T_{n}
.
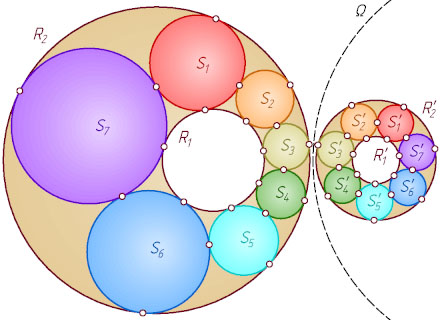
Решение. Рассмотрим случай, когда окружность R_{1}
лежит внутри окружности R_{2}
. При помощи инверсии относительно некоторой окружности \Omega
с центром, не лежащим ни на одной из данных, переведём окружности R_{1}
и R_{2}
в концентрические окружности R_{1}'
и R_{2}'
(см. задачу 6116). При этом цепочка окружностей S_{1}
, S_{2}
, \dots
, S_{n}
перейдёт в цепочку окружностей S_{1}'
, S_{2}'
, \dots
, S_{n}'
одинакового радиуса, каждая из которых касается двух соседних и одной из окружностей R_{1}'
и R_{2}'
внешним образом, а второй — внутренним. Окружность T_{1}
перейдёт в окружность T_{1}'
, касающуюся тем же образом окружностей R_{1}'
и R_{2}'
.
При повороте вокруг общего центра окружностей R_{1}'
и R_{2}'
, переводящем окружность T_{1}'
в S_{1}'
цепочка окружностей S_{1}'
, S_{2}'
, \dots
, S_{n}'
перейдёт в цепочку окружностей T_{1}'
, T_{2}'
, \dots
, T_{n}'
, удовлетворяющую тем же условиям, что и S_{1}'
, S_{2}'
, \dots
, S_{n}'
.
При обратной инверсии окружность T_{1}'
переходит в окружность T_{1}
, а окружности T_{2}'
, T_{3}'
, \dots
, T_{n}'
— в окружности T_{2}
, T_{3}
, \dots
, T_{n}
. При этом цепочка касающихся окружностей T_{1}
, T_{2}
, \dots
, T_{n}
удовлетворяет нужному условию.
Аналогично для остальных возможных случаев расположения исходных окружностей.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — № 227(а), с. 198
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 28.38, с. 191
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 28.40, с. 523
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 154
Источник: Жижилкин И. Д. Инверсия. — (Библиотека «Математическое просвещение». Вып. 35). — М.: МЦНМО, 2009. — с. 54
