6482. Дана окружность и точка A
внутри неё. Найдите геометрическое место вершин C
всевозможных прямоугольников ABCD
, где точки B
и D
лежат на окружности.
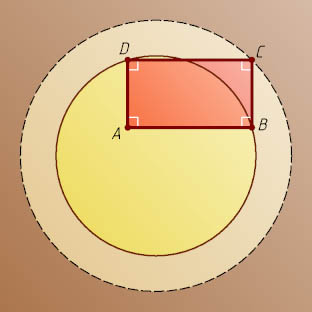
Решение. Воспользуемся следующим утверждением, которое следует из теоремы Пифагора: если ABCD
— прямоугольник, а O
— произвольная точка, то
OA^{2}+OC^{2}=OB^{2}+OD^{2}
(см. задачу 2169).
Пусть O
— центр данной окружности, R
— её радиус, ABCD
— прямоугольник, о котором говорится в условии задачи. Обозначим OA=a
. Поскольку OB=OD=R
и OA^{2}+OC^{2}=OB^{2}+OD^{2}
, то
OC^{2}=OB^{2}+OD^{2}-OA^{2}=2R^{2}-a^{2}.
Значит, точка C
лежит на окружности (обозначим её \Omega
) с центром O
и радиусом \sqrt{2R^{2}-a^{2}}
.
Обратно, пусть C'
— произвольная точка окружности \Omega
. На отрезке AC'
как на диаметре построим окружность. Она пересекает данную окружность в двух точках. Пусть B
— любая из них. Рассмотрим прямоугольник ABCD
, о котором говорится в условии задачи, лежащий по ту же сторону от AB
, что и точка C'
. По ранее доказанному точка C
лежит на окружности \Omega
, а так как CB\perp AB
и C'B\perp AB
, то точки C
и C'
совпадают.
Автор: Панов М. Ю.
Источник: Московская математическая олимпиада. — 2000, LXIII, 9 класс
Источник: Журнал «Квант». — 2000, № 4, с. 47
Источник: Турнир городов. — 1999-2000, XXI, весенний тур, младшие классы, основной вариант
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 3, с. 45
