6527. Точки O_{1}
и O_{2}
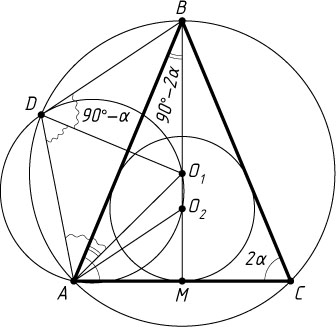
— центры описанной и вписанной окружностей равнобедренного треугольника ABC
(AB=BC
). Окружности, описанные около треугольников ABC
и O_{1}O_{2}A
, пересекаются в точках A
и D
. Докажите, что прямая BD
касается окружности, описанной около треугольника O_{1}O_{2}A
.
Решение. Пусть O_{1}
— центр описанной окружности треугольника ABC
, O_{2}
— центр вписанной окружности этого треугольника, BM
— высота треугольника. Положим \angle BAC=\angle BCA=2\alpha
. Тогда
\angle BAO_{1}=\angle ABO_{1}=90^{\circ}-2\alpha,
Поскольку AO_{2}
— биссектриса угла MAB
, а AO_{2}O_{1}
— внешний угол прямоугольного треугольника AMO_{2}
, то
\angle AO_{2}O_{1}=90^{\circ}+\alpha,
а так как четырёхугольник ADO_{1}O_{2}
вписанный, то
\angle ADO_{1}=180^{\circ}-\angle AO_{2}O_{1}=90^{\circ}-\alpha.
Треугольник AO_{1}D
— равнобедренный (O_{1}A=O_{1}D
как радиусы описанной окружности треугольника ABC
), поэтому
\angle DAO_{1}=\angle ADO_{1}=90^{\circ}-\alpha,
\angle AO_{1}D=180^{\circ}-2(90^{\circ}-\alpha)=2\alpha.
Поскольку AO_{1}D
— центральный угол, а ABD
— вписанный, то
\angle ABD=\frac{1}{2}\angle AO_{1}D=\alpha.
Тогда
\angle BDO_{1}=\angle DBO_{1}=\angle ABD+\angle ABO_{1}=\alpha+(90^{\circ}-2\alpha)=90^{\circ}-\alpha.
Таким образом, \angle BDO_{1}=\angle DAO_{1}
. Тогда по теореме, обратной теореме об угле между касательной и хордой (см. задачу 144), BD
— касательная к окружности, описанной около треугольника O_{1}O_{2}A
.
Автор: Сонкин М. Г.
Источник: Всероссийская олимпиада школьников. — 1996-97, XXIII, окружной этап, 10 класс
Источник: Журнал «Квант». — 1997, № 5, с. 47
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 127, с. 22
