6552. Каждая из окружностей S_{1}
, S_{2}
и S_{3}
касается внешним образом окружности S
(в точках A_{1}
, B_{1}
и C_{1}
соответственно) и двух сторон треугольника ABC
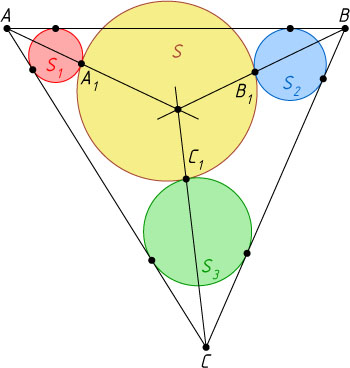
(см.рис.). Докажите, что прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке.
Решение. При гомотетии H_{A_{1}}
, переводящей окружность S_{1}
в окружность S
, прямые AB
и AC
перейдут в параллельные им прямые, касающиеся окружности S
. Точка пересечения A
прямых AB
и AC
перейдёт в некоторую точку A_{2}
пересечения их образов. Значит, точки A
, A_{1}
и A_{2}
лежат на одной прямой.
Аналогично, гомотетии H_{B_{1}}
и H_{C_{1}}
, переводящие S_{2}
и S_{3}
в S
, переводят соответственно прямые AB
, BC
и AC
, BC
в касательные к окружности S
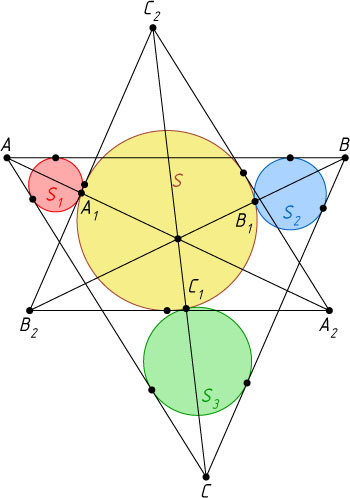
, соответственно параллельные этим прямым. При этом возникает треугольник A_{2}B_{2}C_{2}
, гомотетичный треугольнику ABC
(см. задачу 5000), так как стороны треугольника A_{2}B_{2}C_{2}
соответственно параллельны сторонам треугольника ABC
. Значит, прямые AA_{2}
, BB_{2}
и CC_{2}
пересекаются в одной точке — центре гомотетии, переводящей треугольник ABC
в треугольник A_{2}B_{2}C_{2}
, а так как точки A_{1}
, B_{1}
и C_{1}
лежат соответственно на прямых AA_{2}
, BB_{2}
и CC_{2}
, то прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в этой же точке.
