6574. Четырёхугольник ABCD
с попарно непараллельными сторонами описан около окружности с центром O
. Докажите, что точка O
совпадает с точкой пересечения средних линий четырёхугольника ABCD
тогда и только тогда, когда OA\cdot OC=OB\cdot OD
.
Решение. Пусть точка O
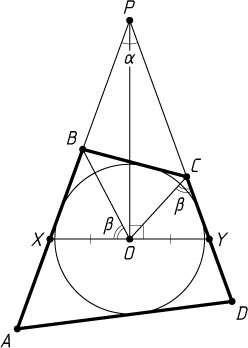
совпадает с точкой пересечения средних линий данного четырёхугольника. Обозначим через X
и Y
середины сторон соответственно AB
и CD
(рис. 1). Поскольку середины сторон любого четырёхугольника являются вершинами параллелограмма (см. задачу 1204), а средние линии четырёхугольника — диагоналями этого параллелограмма, то O
— середина XY
.
Предположим, что прямые AB
и CD
пересекаются в точке P
(пусть, для определённости, точка P
лежит на лучах AB
и DC
). Поскольку PO
— биссектриса и медиана треугольника XPY
, то этот треугольник равнобедренный.
Обозначим, \angle XPY=\alpha
, Тогда
\angle PXY=\angle PYX=90^{\circ}-\frac{\alpha}{2},
а так как BOC
— угол между биссектрисами внешних углов треугольника BPC
, то \angle BOC=90^{\circ}-\frac{\alpha}{2}
(см. задачу 4770). Пусть \angle BOX=\beta
. Тогда
\angle COY=180^{\circ}-\beta-\left(90^{\circ}-\frac{\alpha}{2}\right)=90^{\circ}-\beta+\frac{\alpha}{2},
\angle OCY=180^{\circ}-\angle COY-\angle OYC=
=180^{\circ}-\left(90^{\circ}-\beta+\frac{\alpha}{2}\right)-\left(90^{\circ}-\frac{\alpha}{2}\right)=\beta=\angle BOX.
Значит, треугольники OXB
и CYO
подобны по двум углам. Следовательно, \frac{OB}{OC}=\frac{XB}{YO}
. Аналогично,
\frac{OA}{OD}=\frac{XA}{YO}=\frac{XB}{YO}=\frac{OB}{OC},
откуда следует, что OA\cdot OC=OB\cdot OD
.
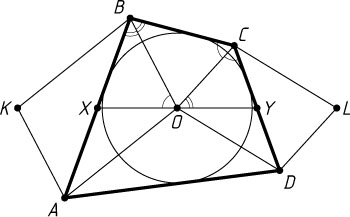
Пусть теперь OA\cdot OC=OB\cdot OD
(рис. 2). Заметим, что
\angle AOB+\angle COD=(180^{\circ}-\angle OAB-\angle OBA)+(180^{\circ}-\angle OCD-\angle ODC)=
=360^{\circ}-\frac{1}{2}(\angle DAB+\angle ABC+\angle BCD+\angle CDA)=180^{\circ}.
Поэтому, если достроить треугольники OAB
и OCD
до параллелограммов AOBK
и OCLD
, то эти параллелограммы будут подобны (так как \frac{OA}{AK}=\frac{OA}{OB}=\frac{DO}{OC}
). Тогда треугольники OXB
и CYO
также будут подобны, поскольку они соответствуют друг другу при подобии параллелограммов. Значит,
\angle XOB=\angle OCY=\angle OCB,~\angle COY=\angle XBO=\angle OBC.
Следовательно,
\angle XOB+\angle BOC+\angle COY=\angle OCB+\angle BOC+\angle OBC=180^{\circ},
т. е. точка O
лежит на прямой XY
. Аналогично, точка O
лежит на прямой, соединяющей середины двух других сторон четырёхугольника, что и требовалось доказать.
Автор: Заславский А. А.
Автор: Исаев М. И.
Автор: Цветов Д.
Источник: Всероссийская олимпиада школьников. — 2004-05, XXXI, заключительный этап, 11 класс
Источник: Журнал «Квант». — 2005, № 5, с. 47
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 735, с. 94

