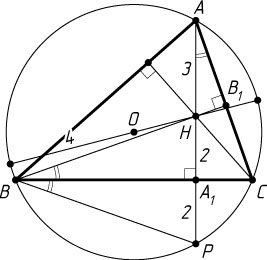
6610. AA_{1}
— высота остроугольного треугольника ABC
, H
— точка пересечения высот, O
— центр окружности, описанной около треугольника ABC
. Найдите OH
, если известно, что AH=3
, A_{1}H=2
, а радиус окружности равен 4.
Ответ. 2.
Решение. Пусть P
— точка пересечения описанной окружности треугольника ABC
с лучом AA_{1}
, R=4
— радиус окружности. Точка, симметричная точке пересечения высот треугольника относительно стороны треугольника, лежит на описанной окружности (см. задачу 4785), поэтому HP=2HA_{1}=4
. По теореме о произведении отрезков пересекающихся хорд
AH\cdot HP=(R-OH)(R+OH),~3\cdot4=R^{2}-OH^{2},~12=16-OH^{2},
откуда OH^{2}=4
. Следовательно, OH=2
.
Автор: Гордин Р. К.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 15.25, с. 151
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 15.25.1, с. 162
Источник: Олимпиада «Высшая проба» (математическая олимпиада ВШЭ). — 2009, заключительный этап, задача 4, 11 класс
