6611. В треугольнике ABC
угол A
равен 60^{\circ}
. Пусть BB_{1}
и CC_{1}
— биссектрисы этого треугольника. Докажите, что точка, симметричная вершине A
относительно прямой B_{1}C_{1}
, лежит на стороне BC
.
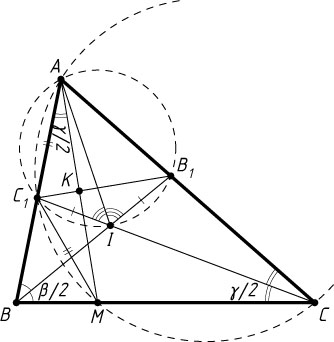
Решение. Первый способ. Пусть I
— точка пересечения биссектрис треугольника ABC
, а прямая, проходящая через вершину A
перпендикулярно B_{1}C_{1}
, пересекает прямые B_{1}C_{1}
и BC
в точках K
и M
соответственно. Обозначим через \beta
и \gamma
углы при вершинах соответственно B
и C
треугольника ABC
. Тогда
\beta+\gamma=120^{\circ},~\frac{\beta}{2}+\frac{\gamma}{2}=60^{\circ},~\angle B_{1}IC_{1}=\angle BIC=90^{\circ}+\frac{1}{2}\angle BAC=90^{\circ}+30^{\circ}=120^{\circ}
(см. задачу 4770), значит, четырёхугольник AB_{1}IC_{1}
вписанный, а так как I
— точка пересечения биссектрис треугольника ABC
, то AI
— биссектриса угла B_{1}AC_{1}
. Следовательно,
IB_{1}=IC_{1},~\angle IC_{1}B_{1}=\angle IB_{1}C_{1}=30^{\circ}.
По теореме о внешнем угле треугольника
\angle AC_{1}B_{1}=\angle ABB_{1}+\angle IB_{1}C_{1}=\frac{\beta}{2}+30^{\circ},
поэтому
\angle C_{1}AM=\angle BAM=\angle C_{1}AK=90^{\circ}-\angle AC_{1}B_{1}=
=90^{\circ}-\left(\frac{\beta}{2}+30^{\circ}\right)=60^{\circ}-\frac{\beta}{2}=\frac{\gamma}{2}=\angle MCC_{1}.
Из точек A
и C
, лежащих по одну сторону от прямой MC_{1}
, отрезок MC_{1}
виден под одним и тем же углом \frac{\gamma}{2}
, значит, точки A
, C
, M
и C_{1}
лежат на одной окружности, а так как CC_{1}
— биссектриса вписанного угла ACM
, то C_{1}A=C_{1}M
, поэтому треугольник AC_{1}M
— равнобедренный. Его высота C_{1}K
является медианой, следовательно, точка M
симметрична точке A
относительно прямой B_{1}C_{1}
. Что и требовалось доказать.
Второй способ. Обозначим \angle ABC=\beta
и \angle ACB=\gamma
. Тогда \beta+\gamma=120^{\circ}
. Пусть I
— точка пересечения биссектрис треугольника ABC
. Тогда (см. задачу 4770)
\angle B_{1}IC_{1}=90^{\circ}+\frac{1}{2}\angle BAC=90^{\circ}+30^{\circ}=120^{\circ}=180^{\circ}-\angle BAC,
поэтому четырёхугольник AC_{1}IB_{1}
вписанный. Значит, учитывая, что AI
— биссектриса угла CAB
, а AIC_{1}
— внешний угол треугольника AIC
, получим
\angle AB_{1}C_{1}=\angle AIC_{1}=\angle CAI+\angle ACI=30^{\circ}+\frac{\gamma}{2}.
Треугольники AB_{1}C_{1}
симметричны относительно прямой B_{1}C_{1}
, поэтому они равны. Тогда
\angle A_{1}B_{1}C_{1}=\angle AB_{1}C_{1}=30^{\circ}+\frac{\gamma}{2},~\angle B_{1}A_{1}C_{1}=\angle B_{1}AC=60^{\circ},
а так как AI
— биссектриса вписанного угла B_{1}AC_{1}
, то IB_{1}=IC_{1}
. Значит,
\angle IB_{1}C_{1}=\angle IC_{1}B_{1}=\angle IAB_{1}=30^{\circ}.
Кроме того,
\angle CB_{1}A_{1}=180^{\circ}-\angle AB_{1}C_{1}-\angle=\angle A_{1}B_{1}C_{1}=
=180^{\circ}-2\angle AB_{1}C_{1}=180^{\circ}-2\left(30^{\circ}+\frac{\gamma}{2}\right)=120^{\circ}-\gamma=\beta.
По свойству биссектрисы треугольника (см. задачу 1509)
\frac{BA}{BC}=\frac{AB_{1}}{B_{1}C}=\frac{A_{1}B_{1}}{B_{1}C},
а так как \angle ABC=\beta=\angle CB_{1}A_{1}
, то треугольники BAC
и B_{1}A_{1}C_{1}
подобны по двум сторонам и углу между ними. Тогда
\angle B_{1}A_{1}C=\angle BAC=60^{\circ}.
Аналогично, \angle C_{1}A_{1}B=60^{\circ}
. Значит,
\angle BA_{1}C=\angle BA_{1}C_{1}+\angle C_{1}A_{1}B_{1}+\angle B_{1}A_{1}C=60^{\circ}+60^{\circ}+60^{\circ}=180^{\circ}.
Следовательно, точка A_{1}
лежит на прямой BC
. Что и требовалось доказать.
Автор: Прокопенко Д. В.
Источник: Всероссийская олимпиада школьников. — 2009-10, XXXVI, региональный этап, 9 класс
Источник: Журнал «Квант». — 2010, № 2, с. 55
Источник: Журнал «Crux Mathematicorum». — 2013, № 10, задача COC98, с. 443
Источник: Молдавские математические олимпиады. — 2011