6617. Диагонали трапеции ABCD
с основаниями AD=3
и BC=1
пересекаются в точке O
. Две окружности, пересекающие основание BC
в точках K
и L
соответственно, касаются друг друга в точке O
, а прямой AD
— в точках A
и D
соответственно. Найдите AK^{2}+DL^{2}
.
Ответ. 12
.
Решение. Из теоремы об угле между касательной и хордой следует, что \angle AKO=\angle OAD=\angle ACK
, поэтому треугольники AKO
и ACK
подобны по двум углам (угол при вершине A
— общий), значит, \frac{AK}{AC}=\frac{AO}{AK}
, откуда AK^{2}=AC\cdot AO
. Аналогично, DL^{2}=BD\cdot DO
.
Треугольник AOD
подобен треугольнику COB
с коэффициентом 3, поэтому AC=\frac{4}{3}AO
и BD=\frac{4}{3}DO
.
Пусть общая касательная к данным окружностям, проведённая через точку O
, пересекает основание AD
в точке M
. Тогда AM=MO=MD
, значит, \angle AOD=90^{\circ}
(см. задачу 1188).
Треугольник AOD
— прямоугольный, следовательно,
AK^{2}+DL^{2}=AC\cdot AO+BD\cdot DO=\frac{4}{3}AO\cdot AO+\frac{4}{3}DO\cdot DO=\frac{4}{3}AO^{2}+\frac{4}{3}DO^{2}=
=\frac{4}{3}(AO^{2}+DO^{2})=\frac{4}{3}AD^{2}=\frac{4}{3}\cdot9=12.
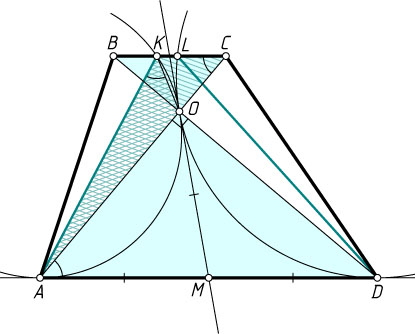
Источник: Математическая олимпиада МГУ «Ломоносов». — 2010, вариант 1, № 10
Источник: Бегунц А. В., Бородин П. А., Горяшин Д. В. и др. Олимпиада школьников «Ломоносов» по математике (2005—2011). — М.: МЦНМО, 2011. — с. 58
