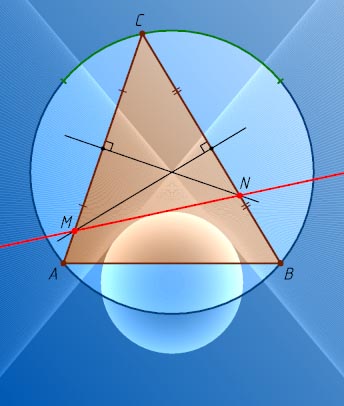
6627. Серединные перпендикуляры к сторонам BC
и AC
остроугольного треугольника ABC
пересекают прямые AC
и BC
в точках M
и N
. Пусть точка C
движется по описанной окружности треугольника ABC
, оставаясь в одной полуплоскости относительно AB
(при этом точки A
и B
неподвижны). Докажите, что прямая MN
касается фиксированной окружности.
Решение. Пусть O
— центр описанной окружности треугольника ABC
. Докажем, что точки A
, O
, N
, B
и M
лежат на одной окружности \omega
.
Обозначим \angle ACB=\gamma
. В четырёхугольнике AOBN
известно, что
\angle OAB=90^{\circ}-\angle ACB=90^{\circ}-\gamma,
\angle ONB=180^{\circ}-\angle CNK=180^{\circ}-(90^{\circ}-\gamma)=90^\circ+\gamma.
Тогда
\angle OAB+\angle ONB=(90^{\circ}-\gamma)+(90^{\circ}+\gamma)=180^{\circ}.
Следовательно, точки A
, B
, O
и N
лежат на некоторой окружности \omega
. Аналогично можно показать, что четырёхугольник AOBM
тоже вписанный, т. е. точка M
лежит на окружности \omega
. Следовательно, точки A
, O
, N
, B
и M
лежат на окружности \omega
.
Поскольку точки A
, B
, O
фиксированы, то окружность \omega
— фиксирована. Кроме того,
\angle MON=180^{\circ}-\angle ACB=180^{\circ}-\gamma=\mbox{const}.
Следовательно, длина хорды MN
окружности \omega
постоянна и не зависит от положения точки C
. Все такие хорды находятся на одном расстоянии от центра P
окружности \omega
(см. задачу 1673), а значит, касаются некоторой окружности \omega_{0}
с центром P
.
Примечание. 1. Если P
— центр окружности \omega
, а OQ
— её диаметр, то \angle OAQ=\angle OBQ=90^{\circ}
, поэтому QA
и QB
— касательные к описанной окружности треугольника ABC
, т. е. касательные к описанной окружности треугольника ABC
, проведённые в точках A
и B
, пересекаются на окружности \omega
.
Кроме того, из теоремы об угле между касательной и хордой следует, что \angle BAQ=\angle ACB=\gamma
, значит, QA=QB=MN
, поэтому QA
и QB
также касаются окружности \omega'
. Пусть E
— точка касания QA
и \omega'
. Тогда PE
— средняя линия треугольника QAO
. Следовательно, радиус окружности \omega'
вдвое меньше радиуса описанной окружности треугольника ABC
.
2. Утверждение задачи остаётся верным для тупоугольного треугольника ABC
(точка C
может быть расположена в любой из двух полуплоскостей с границей AB
).
Автор: Прокопенко Д. В.
Источник: Московская устная олимпиада по геометрии. — 2010, № 6, 8-9 классы
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2010, VI, 11 апреля
